Kas yra trupmena su vienu kintamuoju?
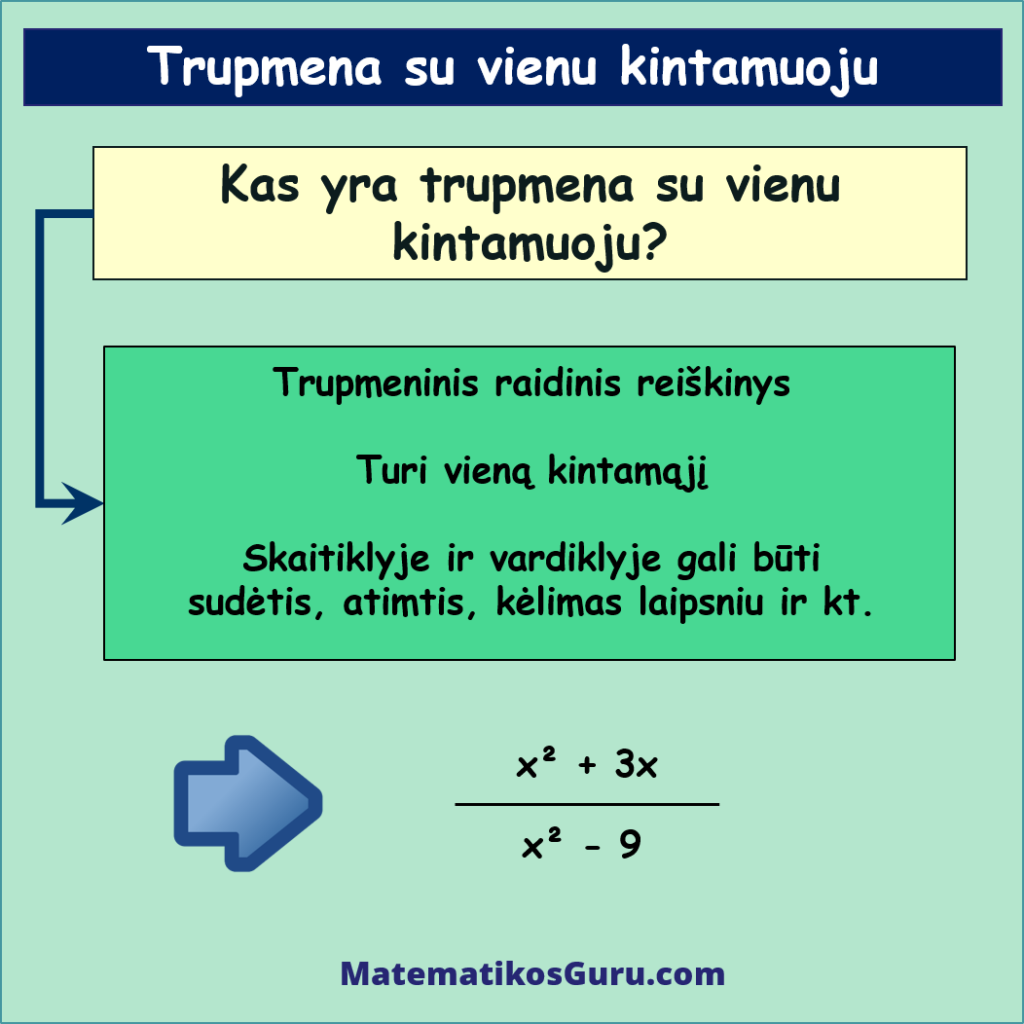
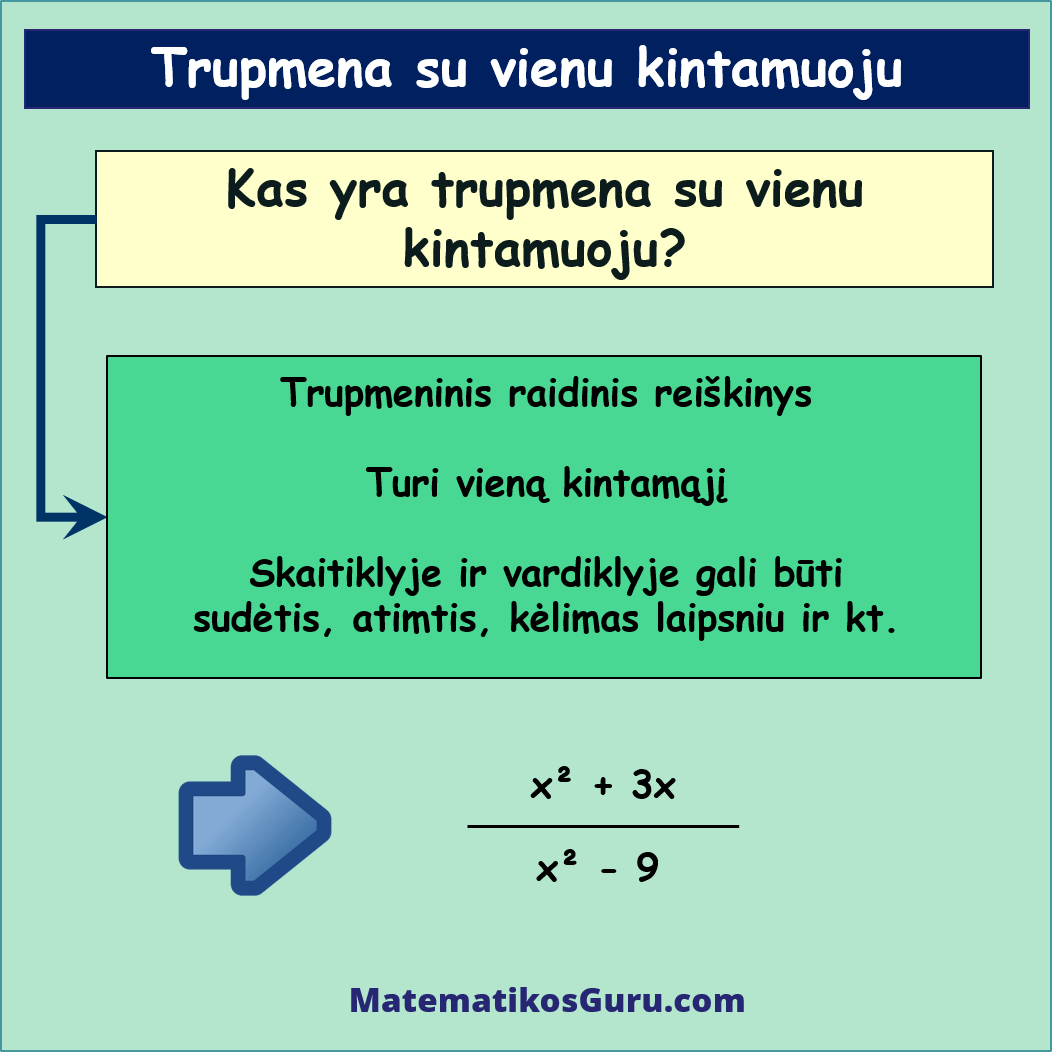
![]() Trupmena su vienu kintamuoju – tai trupmeninis raidinis reiškinys, kuris turi vieną kintamąjį. Šis kintamasis žymimas raide, pavyzdžiui x, ir jis yra dalies vardiklyje ir (arba) skaitiklyje. Iš esmės tai trupmena, bet ji yra sudėtingesnė nei paprastos skaitinės trupmenos, kadangi jų skaitiklyje ar vardiklyje gali būti kintamieji, kėlimas laipsniu, daugyba, sudėtis ar atimtis.
Trupmena su vienu kintamuoju – tai trupmeninis raidinis reiškinys, kuris turi vieną kintamąjį. Šis kintamasis žymimas raide, pavyzdžiui x, ir jis yra dalies vardiklyje ir (arba) skaitiklyje. Iš esmės tai trupmena, bet ji yra sudėtingesnė nei paprastos skaitinės trupmenos, kadangi jų skaitiklyje ar vardiklyje gali būti kintamieji, kėlimas laipsniu, daugyba, sudėtis ar atimtis.
Pavyzdys:
Panagrinėkime pavyzdį. Duota trupmena su vienu kintamuoju:
- x2 + 3xx2 – 9
Kaip matote, tai yra raidinis reiškinys su vienu nežinomuoju x, kuris yra tiek vardiklyje, tiek skaitiklyje. Trupmenos reikšmė priklauso nuo kintamojo x reikšmės.

Svarbu!
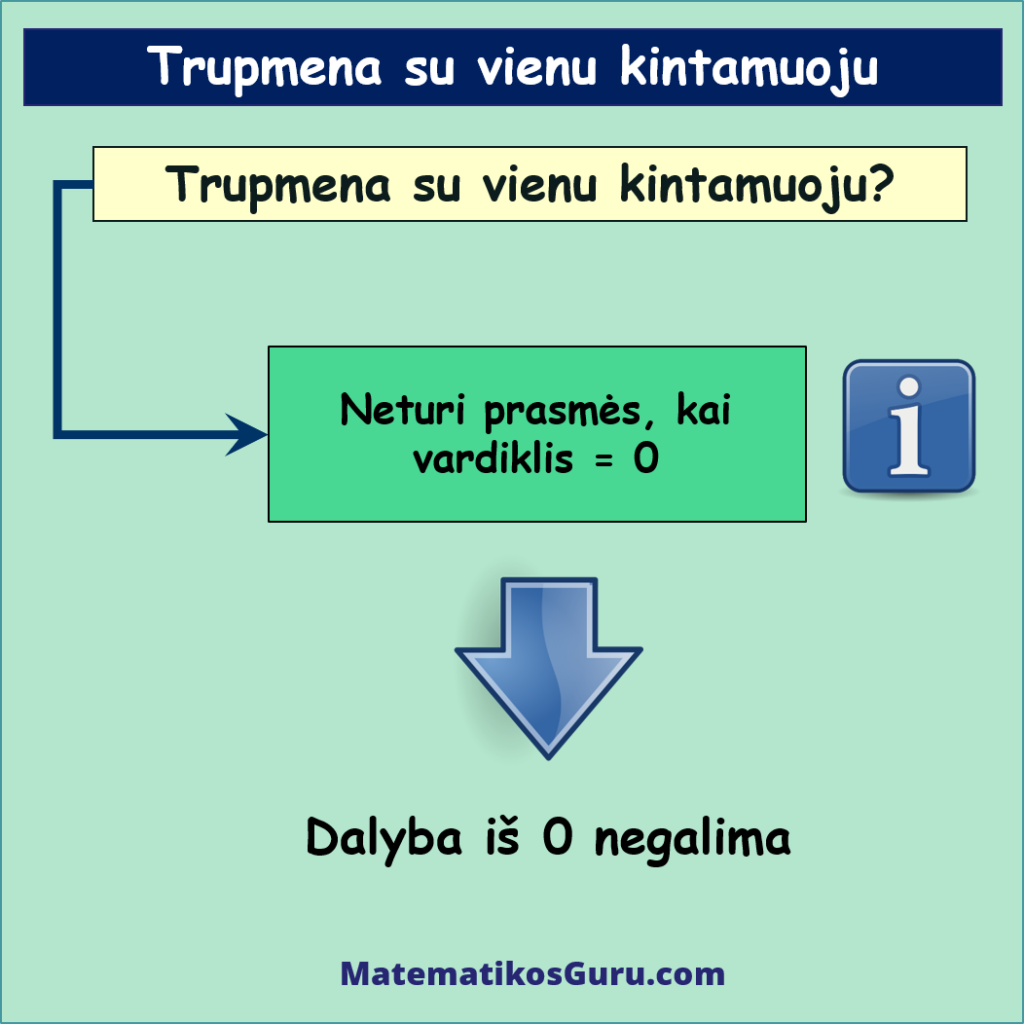
Trupmena neturi prasmės tuo atveju, jeigu vardiklis yra lygus 0. Taip yra todėl, kad dalyba iš 0 negalima
Kaip suprastinti trupmeną su vienu kintamuoju?
Visų pirma svarbu suprasti, kodėl būtina mokėti suprastinti trupmeną su vienu kintamuoju
- Aiškumas ir lengvesnis supratimas: suprastinti reiškiniai yra lengviau suprantami, yra aiškesni. Sudėtingi reiškiniai gali slėpti svarbias savybes ir ryšius, kurie tampa akivaizdūs tik supaprastinus šiuos reiškinius
- Lengvesnis uždavinių sprendimas: suprastinti reiškiniai dažnai leidžia leidžia lengviau spręsti lygtis ar nelygybes, kadangi suprastinimo metu yra atsikratoma nereikalingų sudedamųjų reiškinio dalių, kas palengvina aritmetinių veiksmų atlikimą
Toliau yra pateiktas paaiškinimas, kaip yra suprastinama trupmena su vienu kintamuoju:
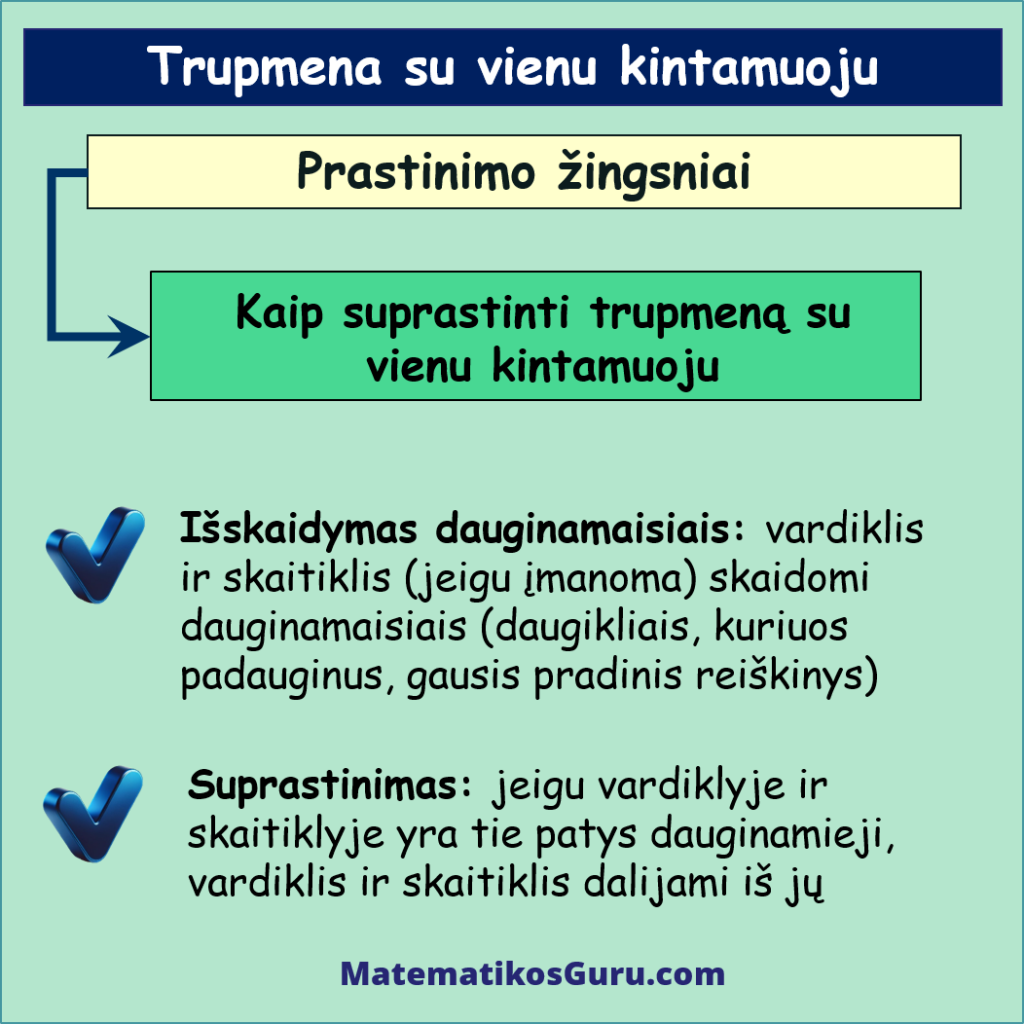
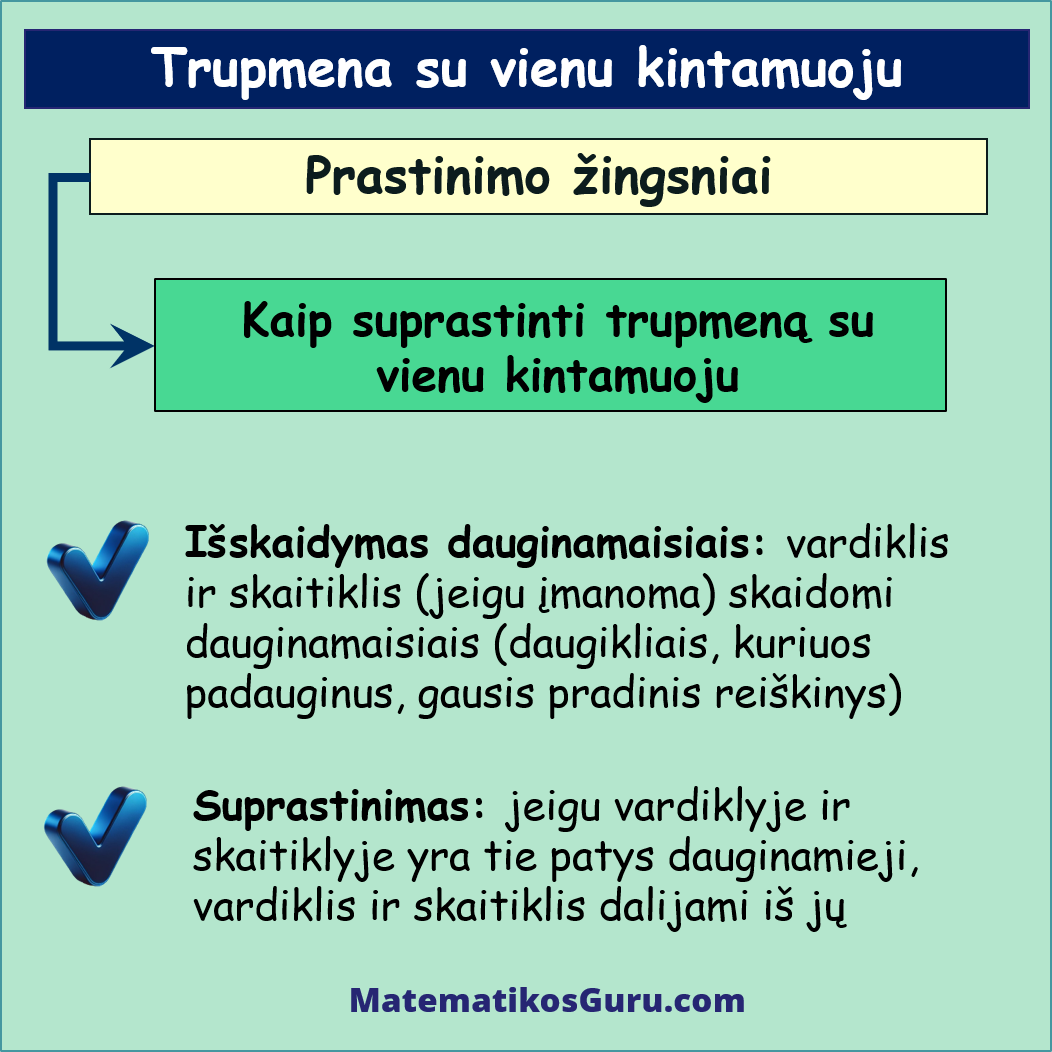
- Išskaidymas dauginamaisiais: visų pirma, jei įmanoma, išskaidykite skaitiklio ir vardiklio raidinius reiškinius dauginamaisiais. Čia jums labai padės greitosios daugybos formulės. Tai reiškia, kad reikia rasti tiek skaitiklio, tiek vardiklio daugiklius, kuriuos padauginus tarpusavyje, gautųsi pradinė reiškinio išraiška
- Suprastinimas: tikriname, ar skaitiklyje ir vardiklyje yra tas pats ar tie patys dauginamieji. Jeigu tokie yra, tiek skaitiklis, tiek vardiklis dalijami iš to dauginamojo (iš tų dauginamųjų)
Panagrinėkime keletą pavyzdžių:
![]() Pavyzdys 1
Pavyzdys 1
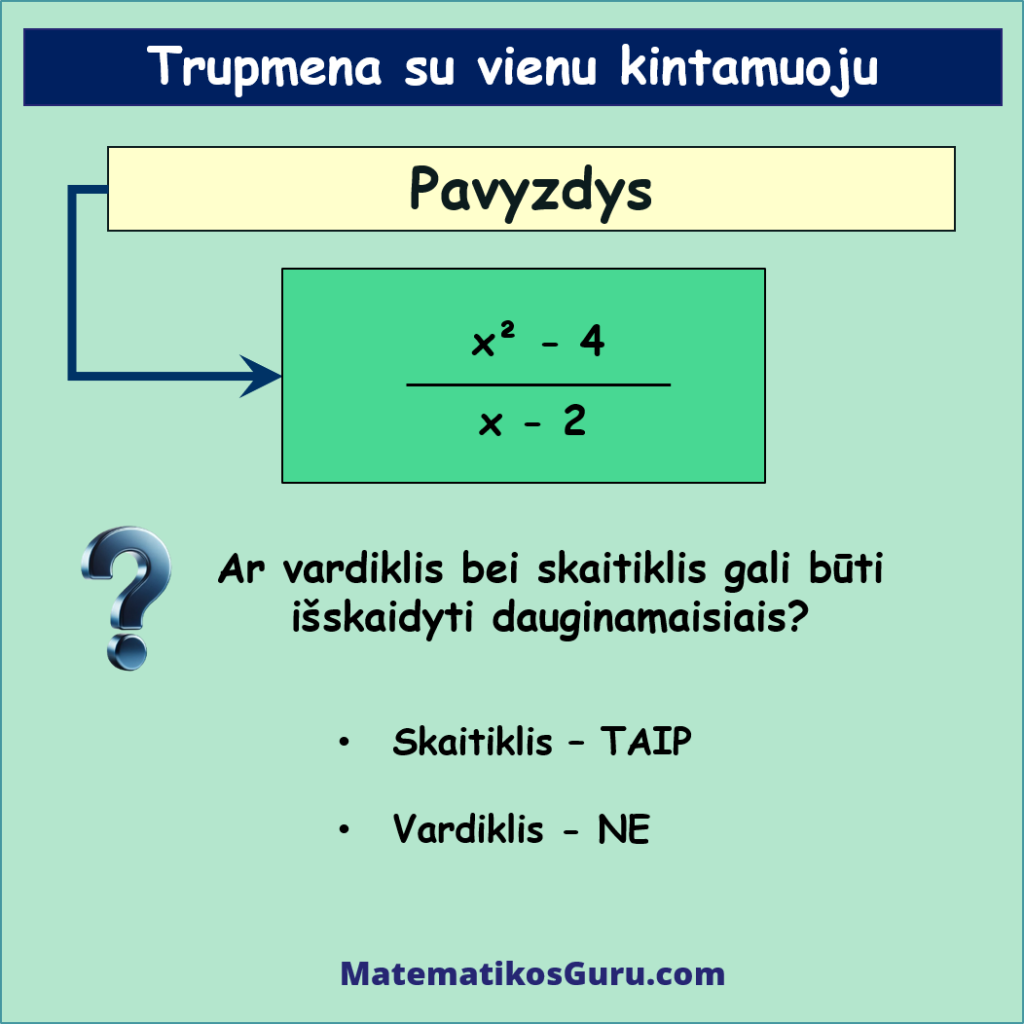
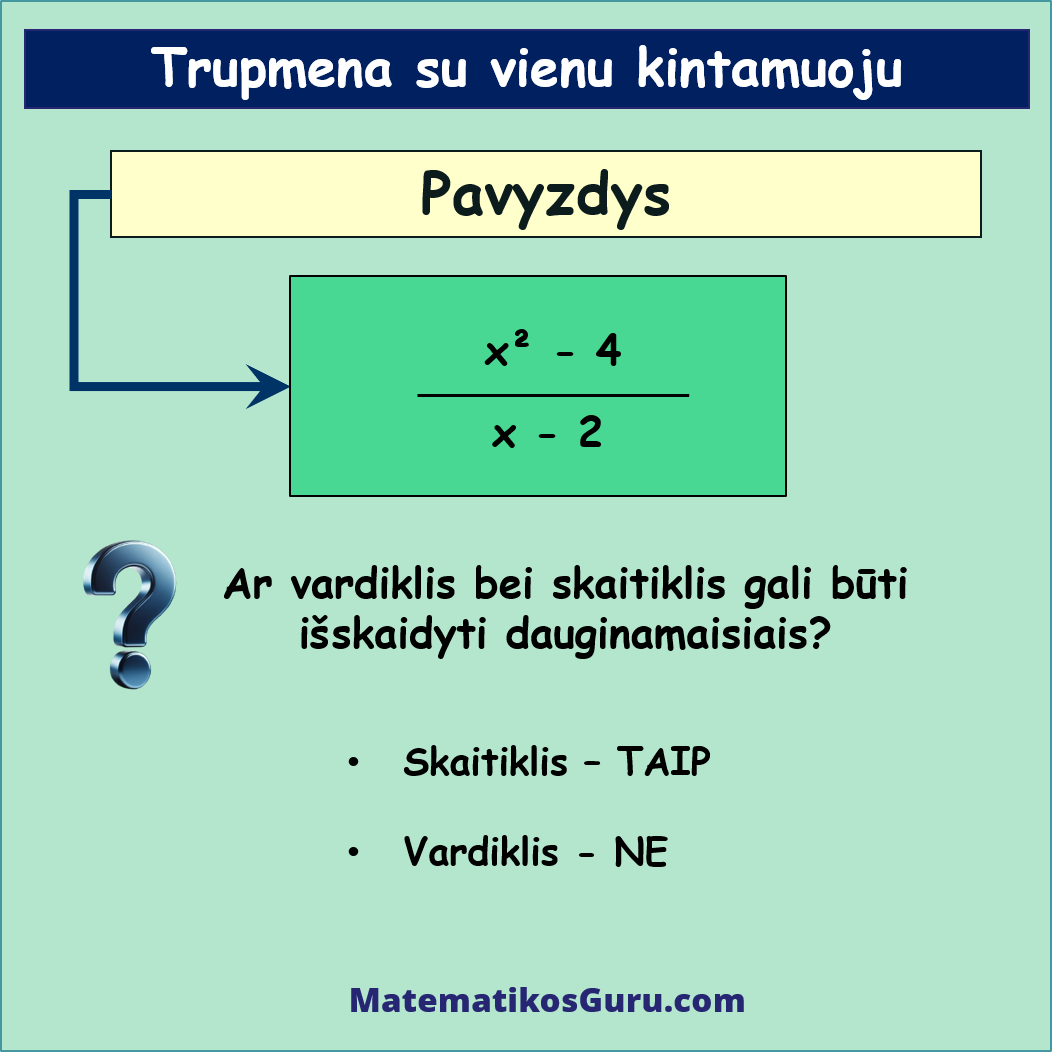
Duota tokia trupmena su vienu kintamuoju: x2 – 4x – 2. Suprastinkime ją
Tikriname ar galime tiek skaitiklį, tiek vardiklį išskaidyti dauginamaisiais?
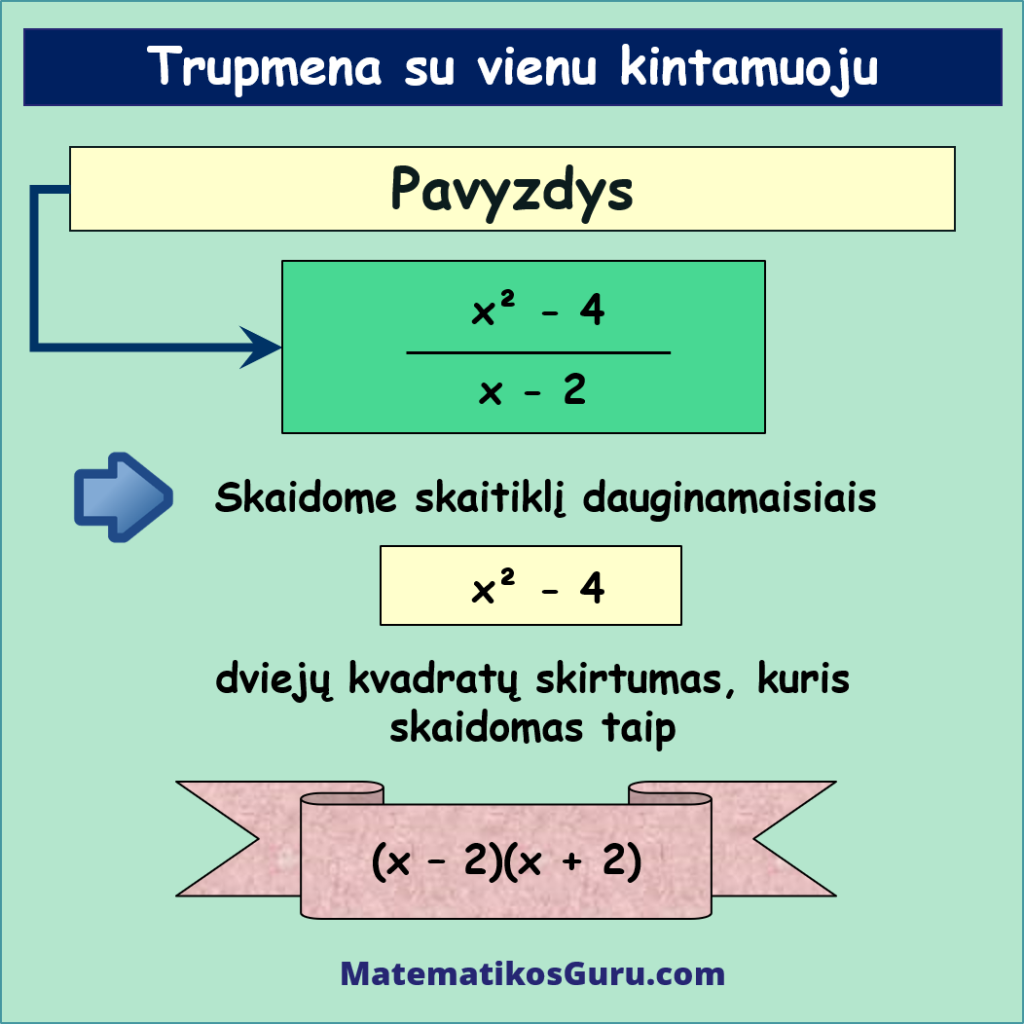
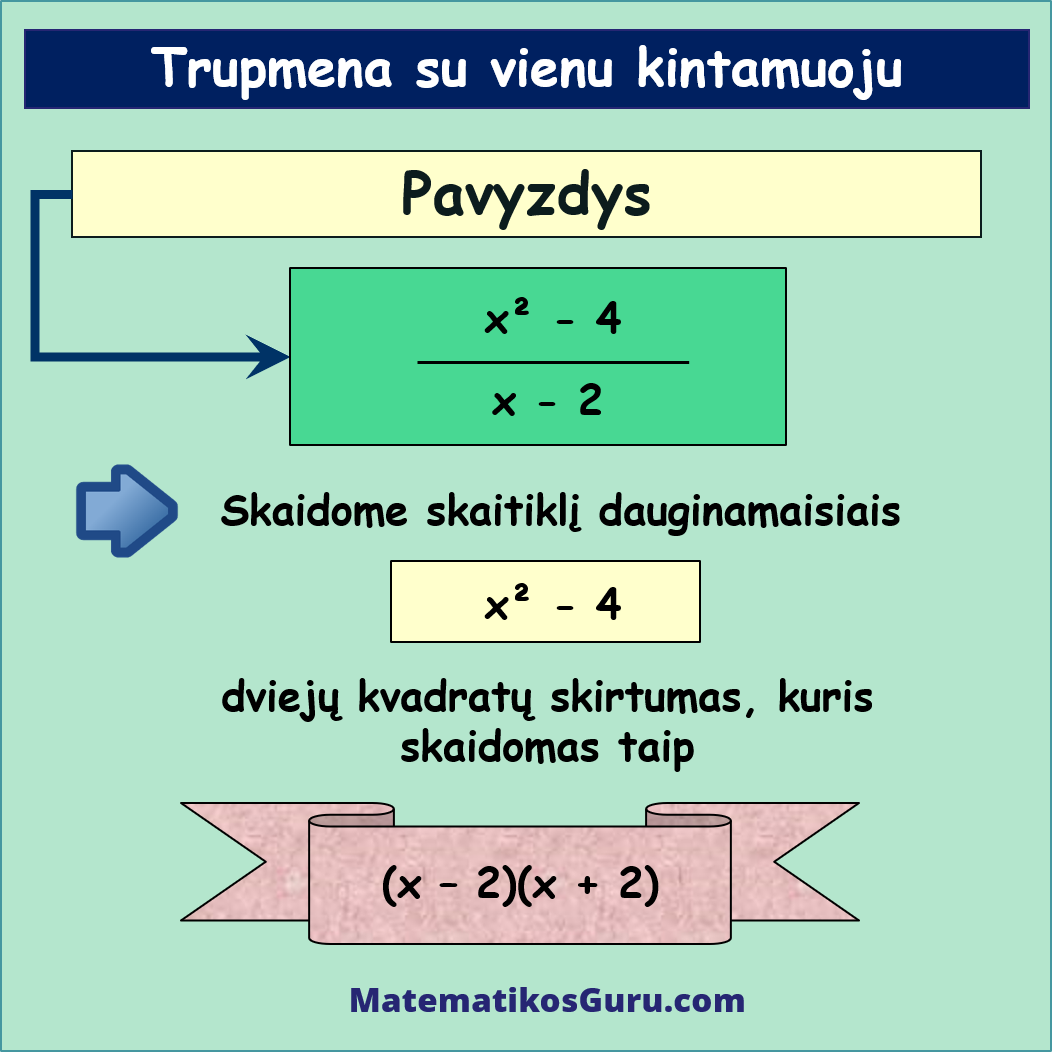
- Skaitiklyje esantis raidinis reiškinys yra dviejų kvadratų skirtumas, t.y. x2 – 4. Pritaikę greitosios daugybos formules, šį reiškinį galite išskaidyti į dviejų dauginamųjų sandaugą, t.y. (x – 2)(x + 2)
Atlikę šį veiksmą, turime tokį reiškinį:
- (x – 2)(x + 2)x – 2.
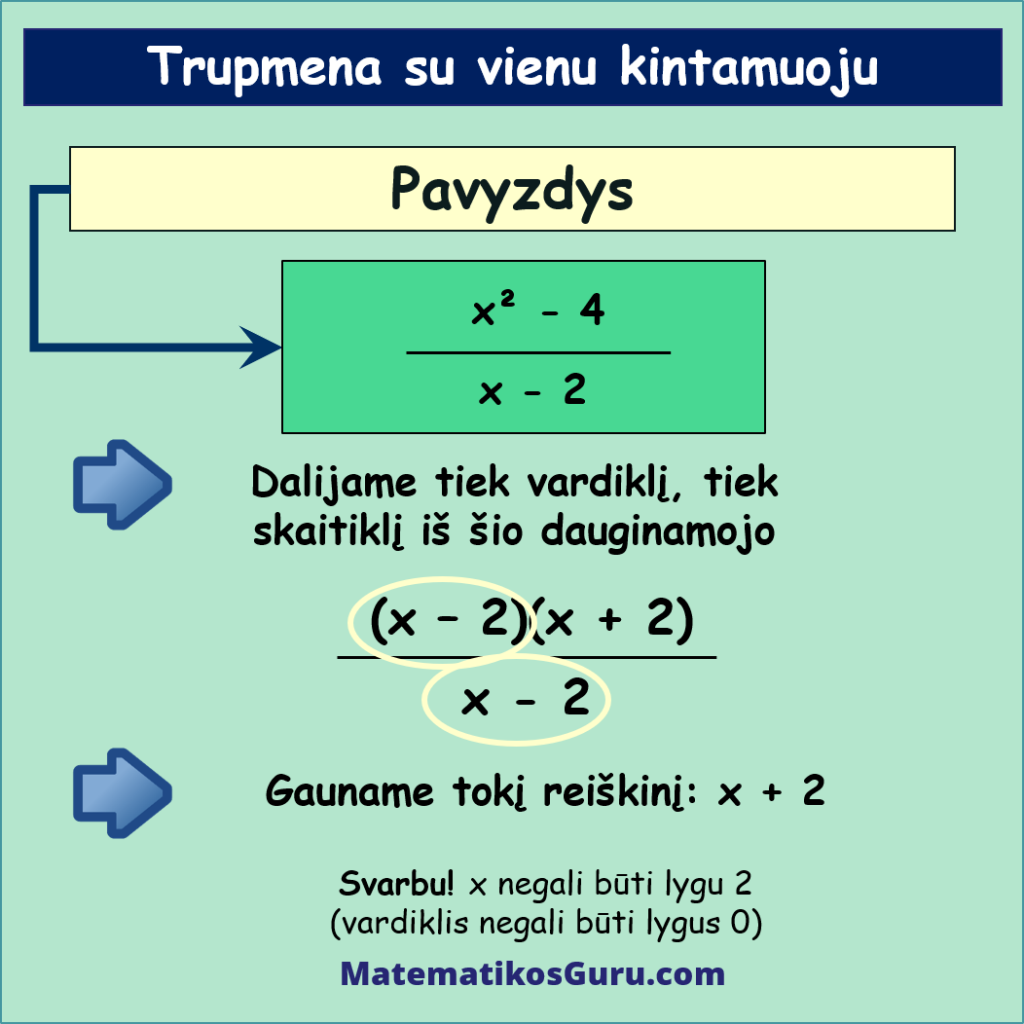
Matome, kad tiek skaitiklyje, tiek vardiklyje yra vienodas dauginamasis x – 2. Dalijame tiek skaitiklį, tiek vardiklį iš šio dauginamojo ir suprastiname trupmeną.
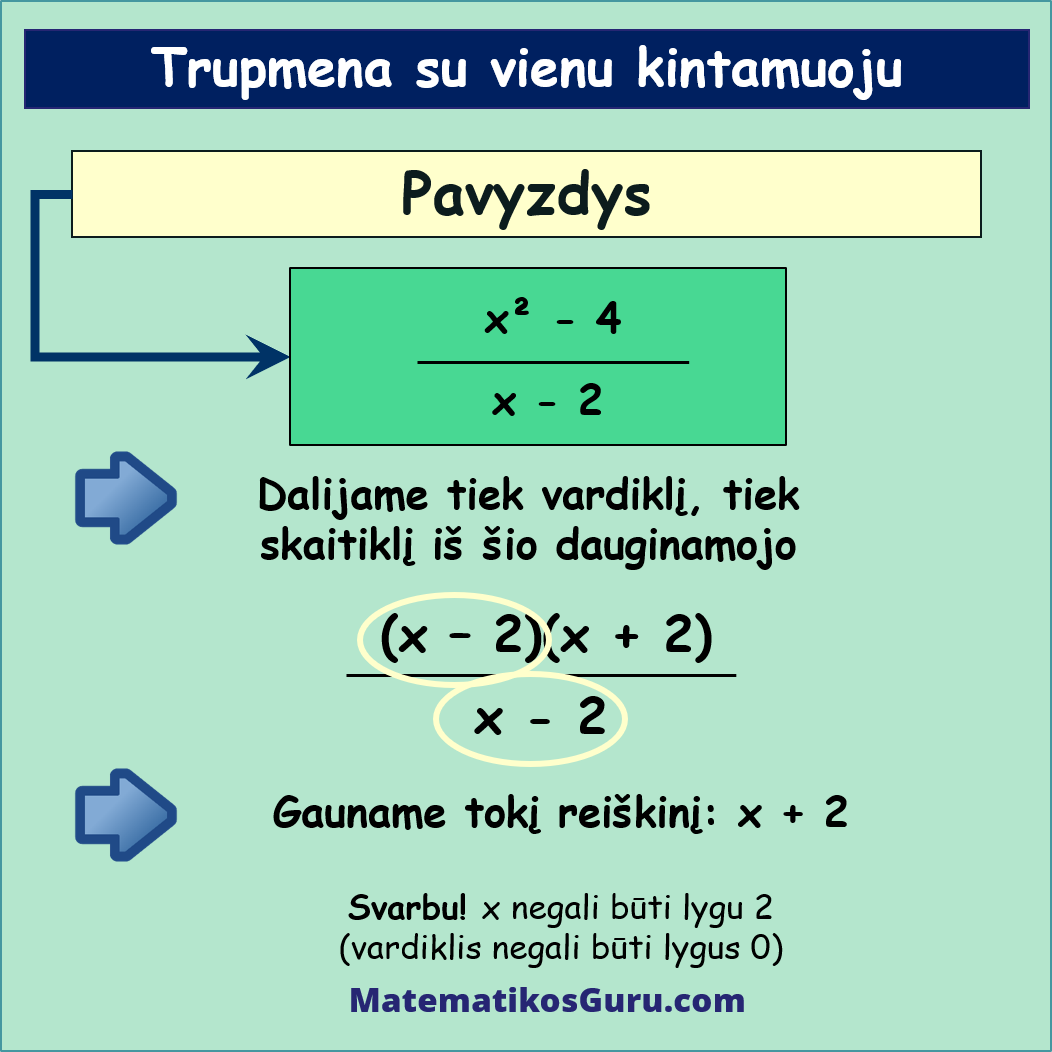
Gauname tokį suprastintą reiškinį: x + 2
![]() Pavyzdys 2
Pavyzdys 2
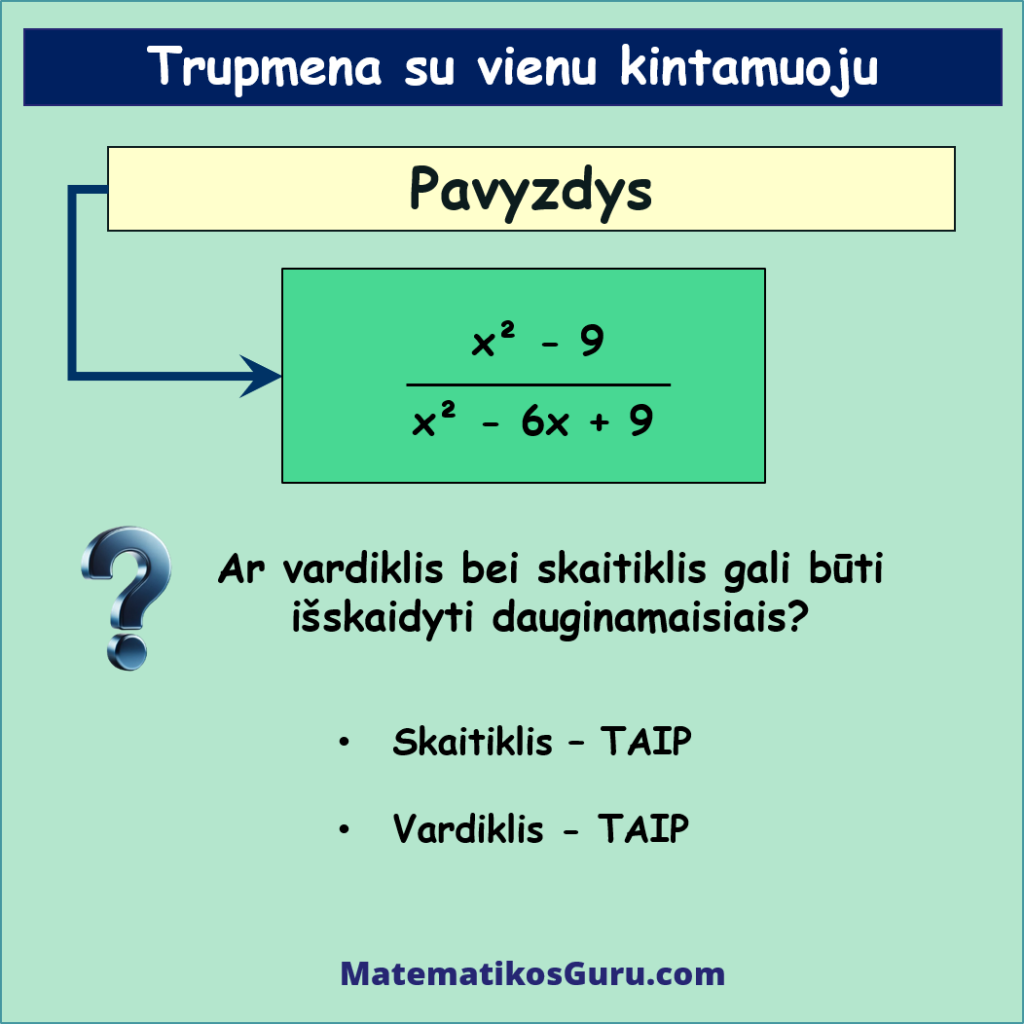
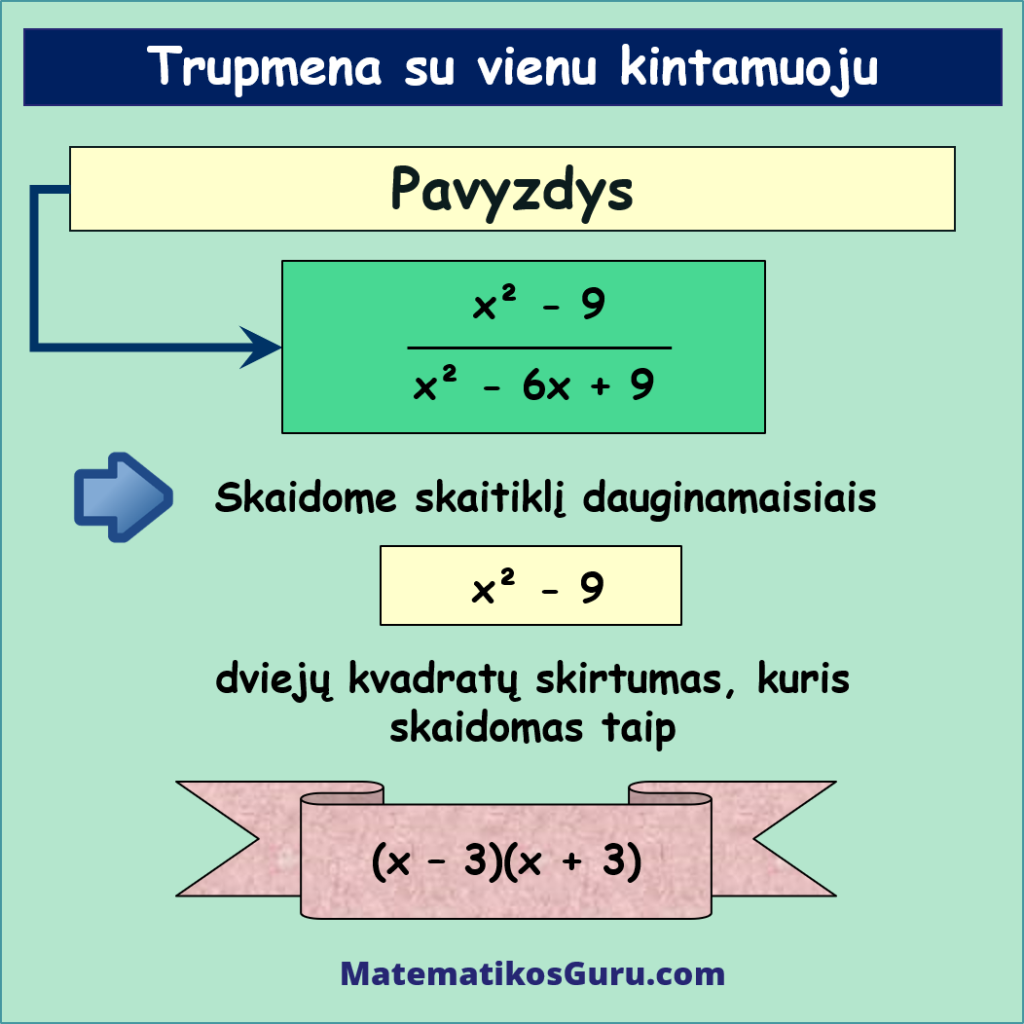
Duota tokia trupmena su vienu kintamuoju: x2 – 9x2 – 6x + 9. Suprastinkime ją
Tikriname ar galime tiek skaitiklį, tiek vardiklį išskaidyti dauginamaisiais?
- Skaitiklyje esantis raidinis reiškinys yra dviejų kvadratų skirtumas, t.y. x2 – 9. Pritaikę greitosios daugybos formules, šį reiškinį galite išskaidyti į dviejų dauginamųjų sandaugą, t.y. (x – 3)(x + 3)
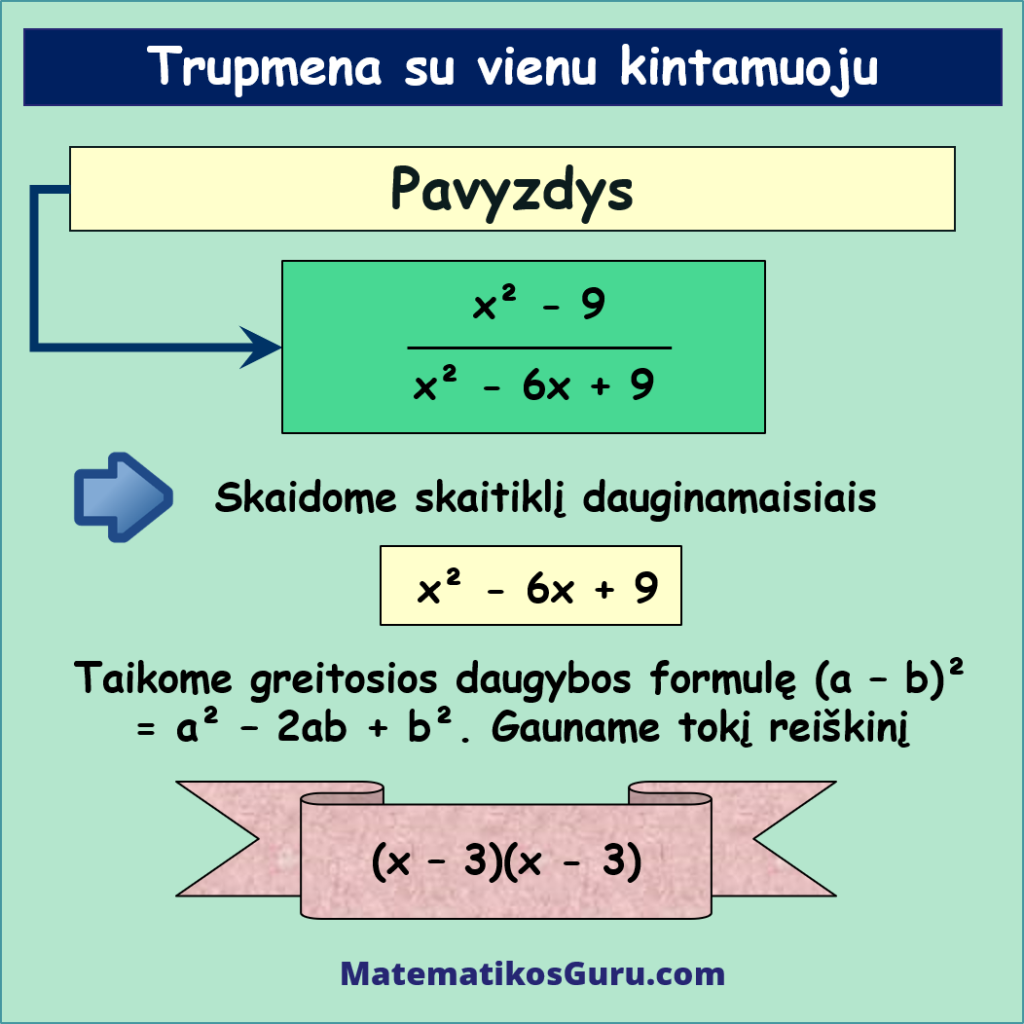
- Vardiklyje esantis reiškinys taip pat gali būti išskaidytas dauginamaisiais (taikykite greitosios daugybos formules – šiuo atveju (a – b)² = a² – 2ab + b²). Taikydami šią formulę vardiklyje esančiam raidiniam reiškiniu, gauname tokį rezultatą: x2 – 6x + 9 = (x – 3)2 arba (x – 3)(x – 3)
Atlikę šiuos veiksmus, gauname tokią trupmeną:
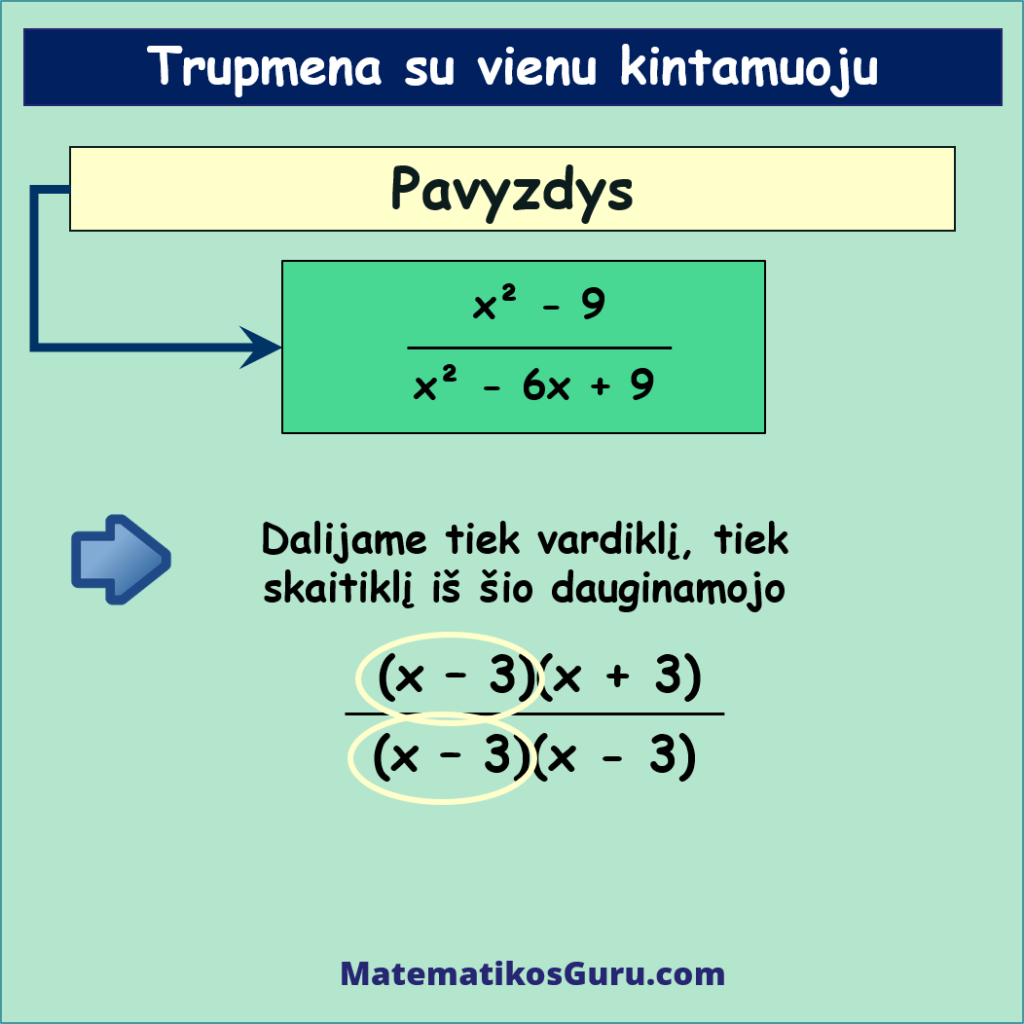
- (x – 3)(x + 3)(x – 3)(x – 3)
Matome, kad tiek skaitiklyje, tiek vardiklyje yra vienodas dauginamasis x – 3. Dalijame tiek skaitiklį, tiek vardiklį iš šio dauginamojo ir suprastiname trupmeną.

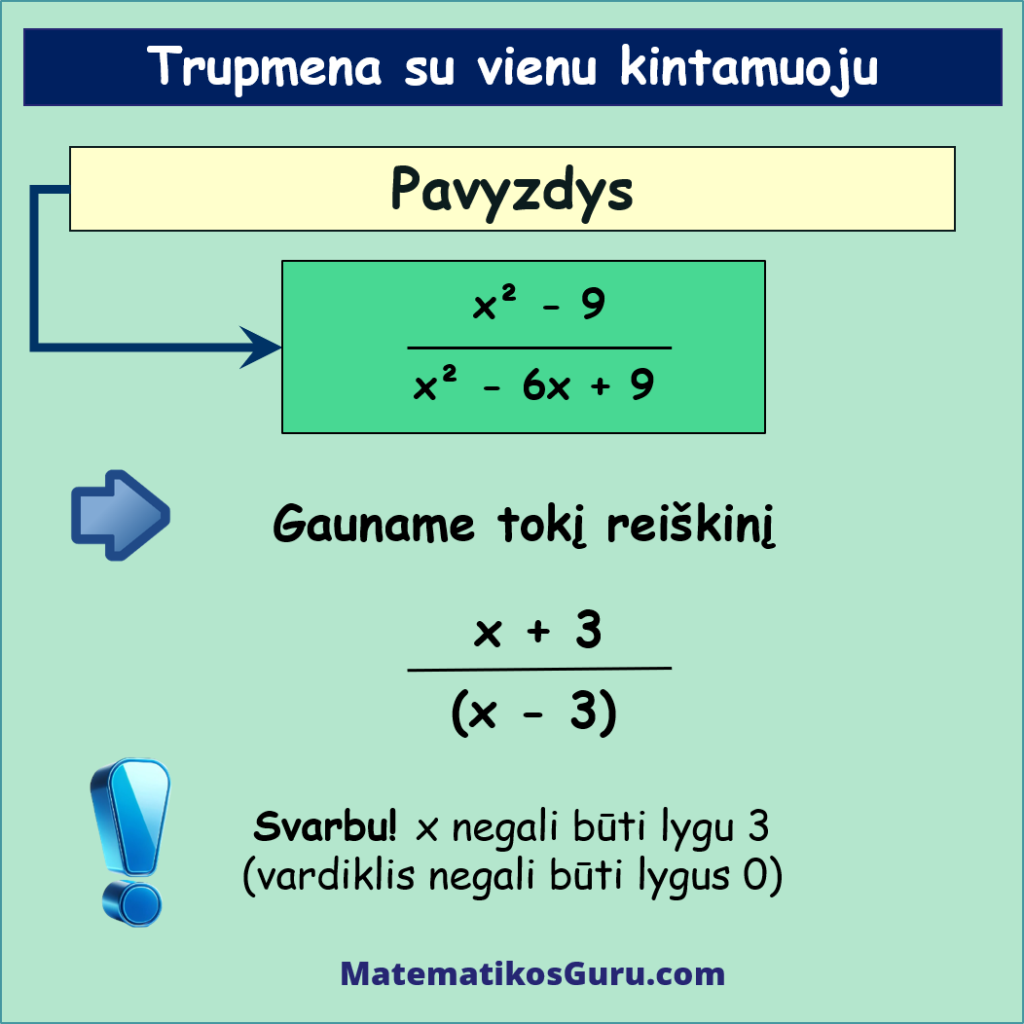
Gauname tokį suprastintą reiškinį: x + 3x – 3.
 Svarbu!
Svarbu!
x reikšmės negali būti tokios, kurioms esant trupmenos vardiklis yra lygus 0. Šiuo atveju x negali būti lygu 3.
Vaizdinė medžiaga
Populiariausios temos:
Grįžkite iš Prastiname trupmenas su vienu kintamuoju temos į MatematikosGuru.com pradžią