Pitagoro teoremos nagrinėjimas pradedamas nuo stačiojo trikampio sąvokos
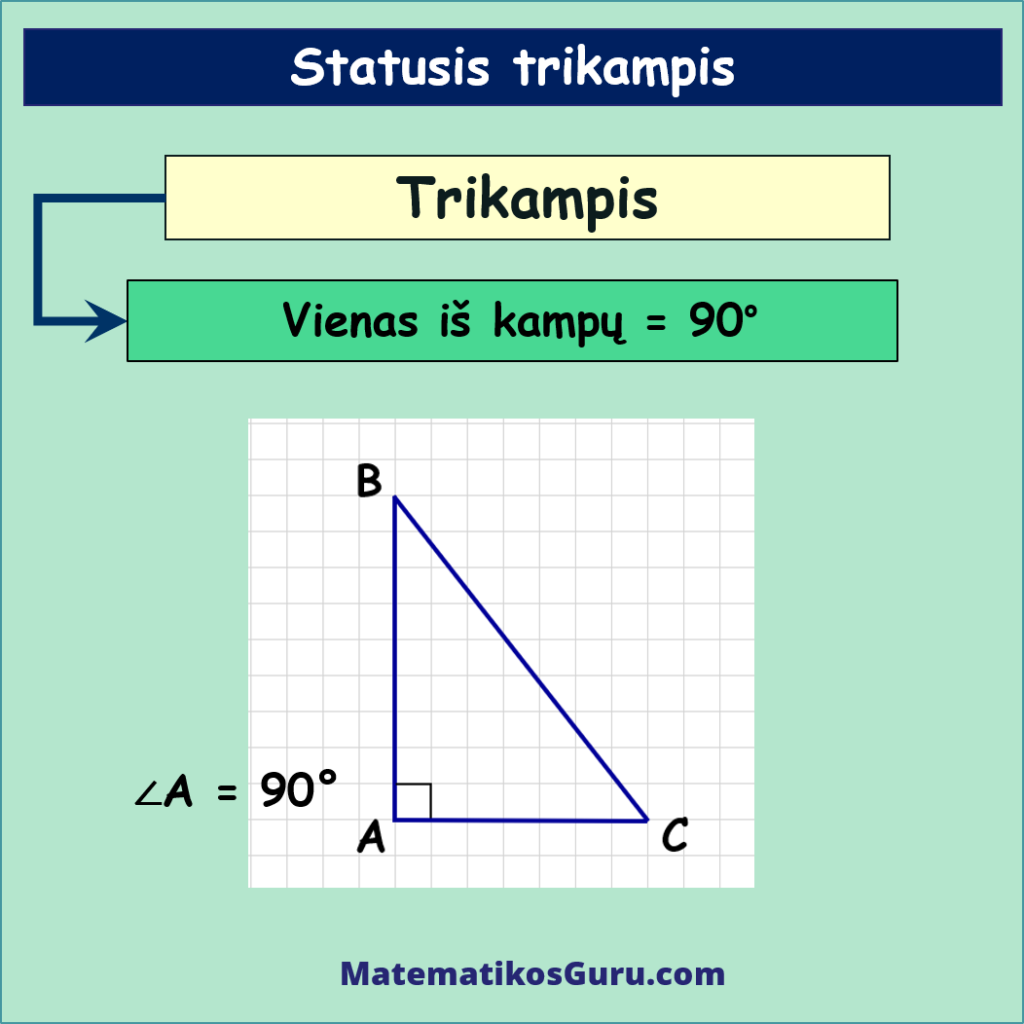
- Statusis trikampis – tai trikampis, kurio vienas iš trijų kampų yra status, t.y. ∠A = 90°, trikampis △ABC – statusis
Kitų dviejų stačiojo trikampio kampų suma yra 90°, t.y. ∠B + ∠C = 90°
Pitagoro teoremos nagrinėjimui taip pat reikalingos šios sąvokos:
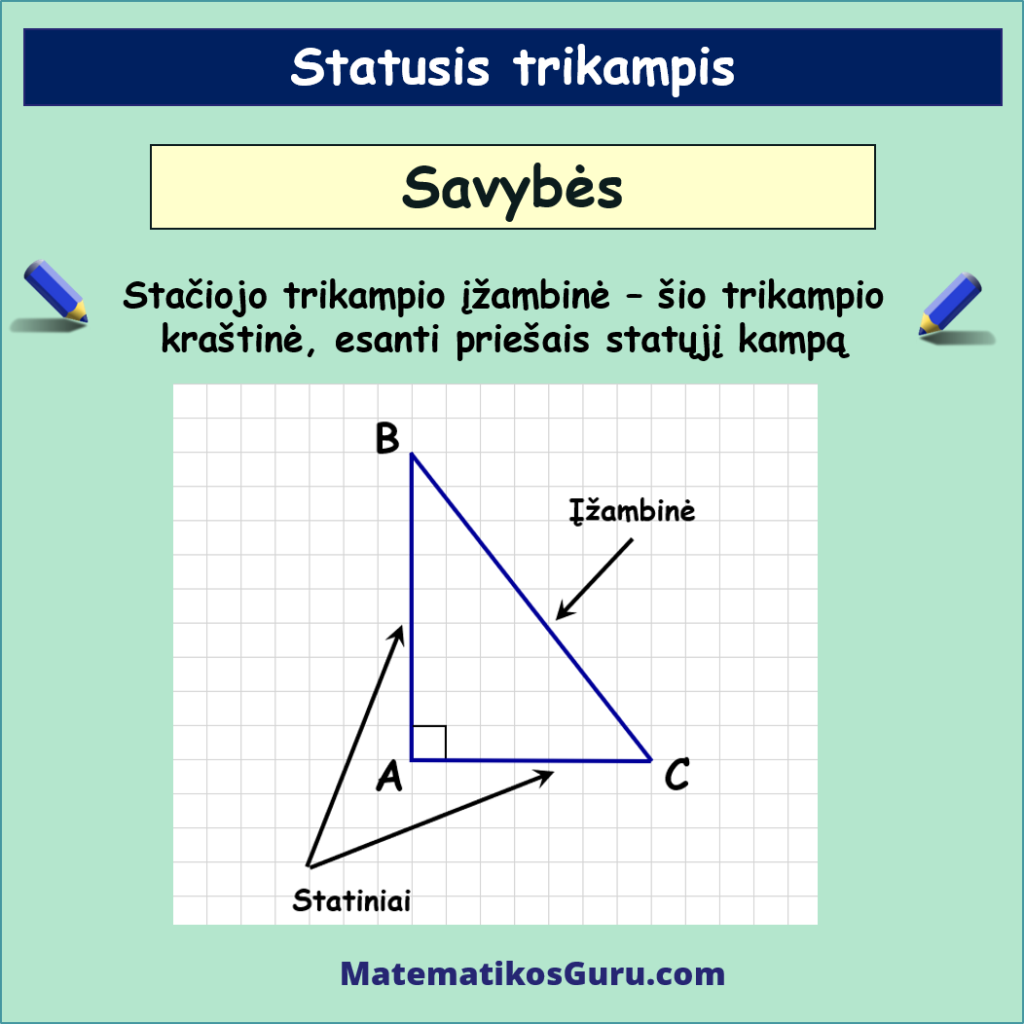
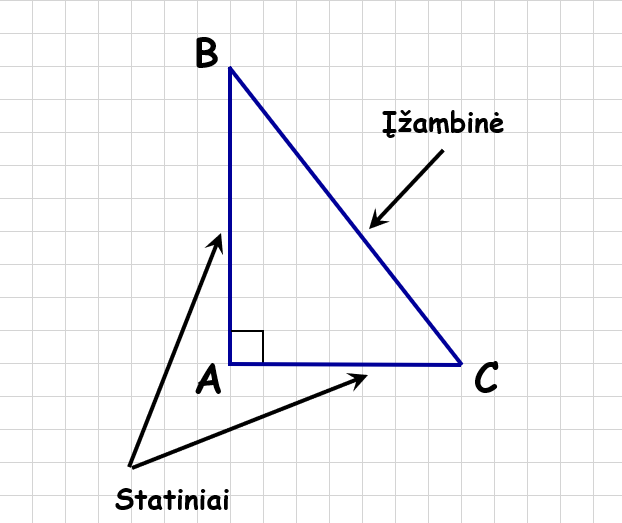
- Stačiojo trikampio įžambinė – šio trikampio kraštinė, esanti priešais statųjį kampą – BC
- Stačiojo trikampio statiniai – šio trikampio kraštinės, kurios sudaro statųjį kampą, AB ir AC
Pitagoro teorema
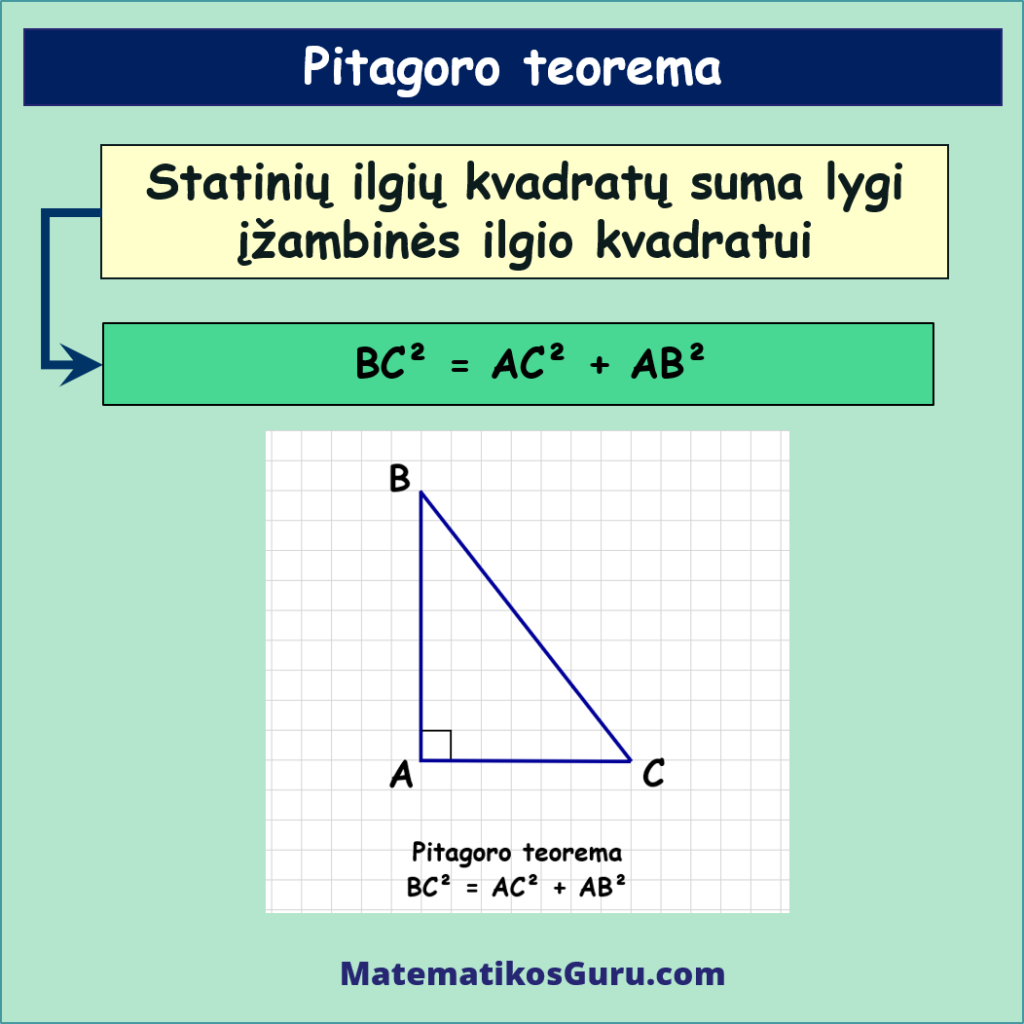
 Pitagoro teorema – stačiojo trikampio statinių ilgių kvadratų suma lygi įžambinės ilgio kvadratui
Pitagoro teorema – stačiojo trikampio statinių ilgių kvadratų suma lygi įžambinės ilgio kvadratui
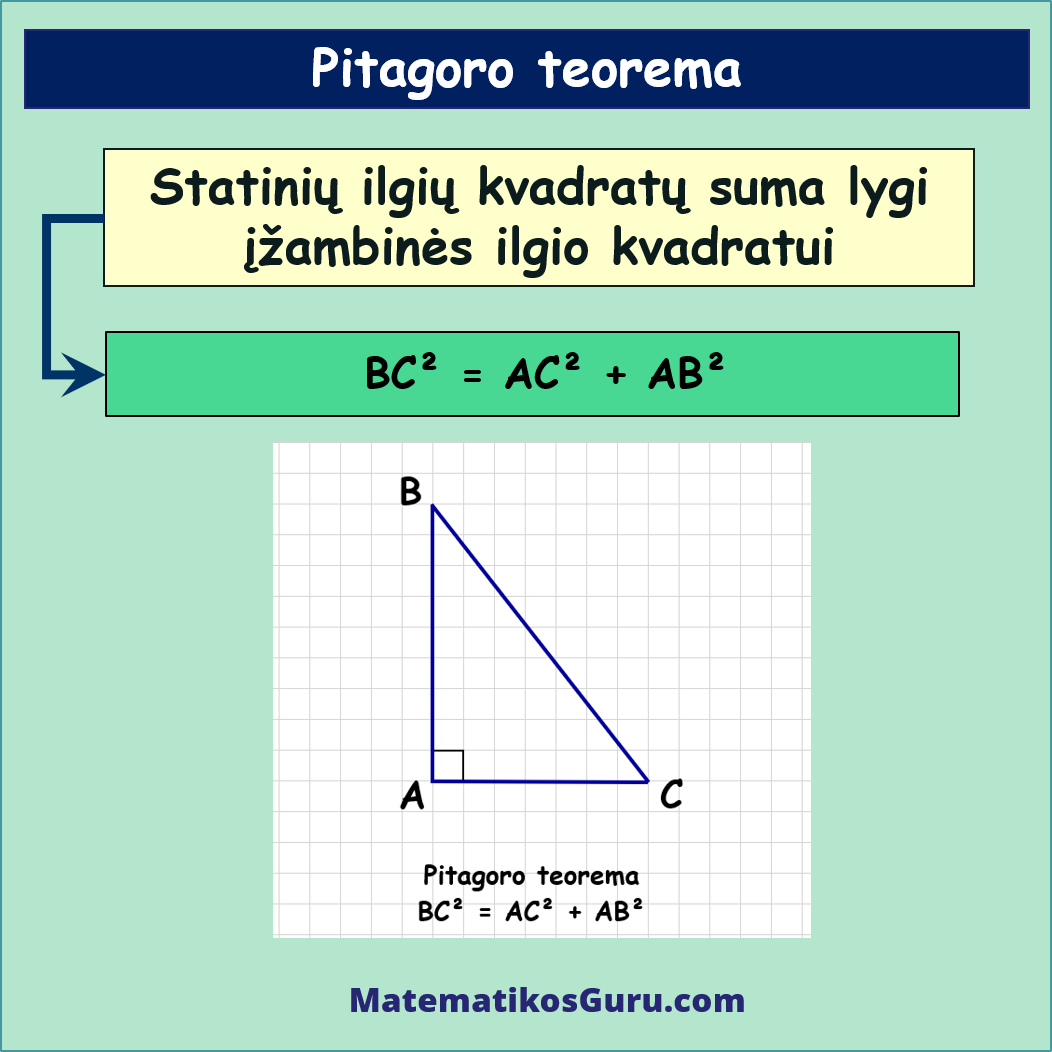
Pitagoro teorema – formulė yra tokia:
BC² = AC² + AB²
Tuo atveju, jeigu žinome stataus trikampio statinių ilgius, galime apskaičiuoti šio trikampio įžambinės ilgį. Tuo atveju, jeigu žinome vieną iš stataus trikampio statinių ilgį ir įžambinės ilgį, galime apskaičiuoti antrojo statinio ilgį.
Pavyzdžiai:
![]() Pavyzdys 1:
Pavyzdys 1:
Stačiojo trikampio statinių ilgiai yra 3 cm ir 4 cm. Apskaičiuokite šio trikampio įžambinės ilgį.
Pažymėkime vieną statinį raide a, o kitą – raide b, o įžambinę – raide c. Taikydami Pitagoro teoremą, gauname tokią lygtį: a2 + b2 = c2, kur:
- a – vieno iš statinių ilgis
- b – kito iš dviejų statinių ilgis
- c – įžambinės ilgis
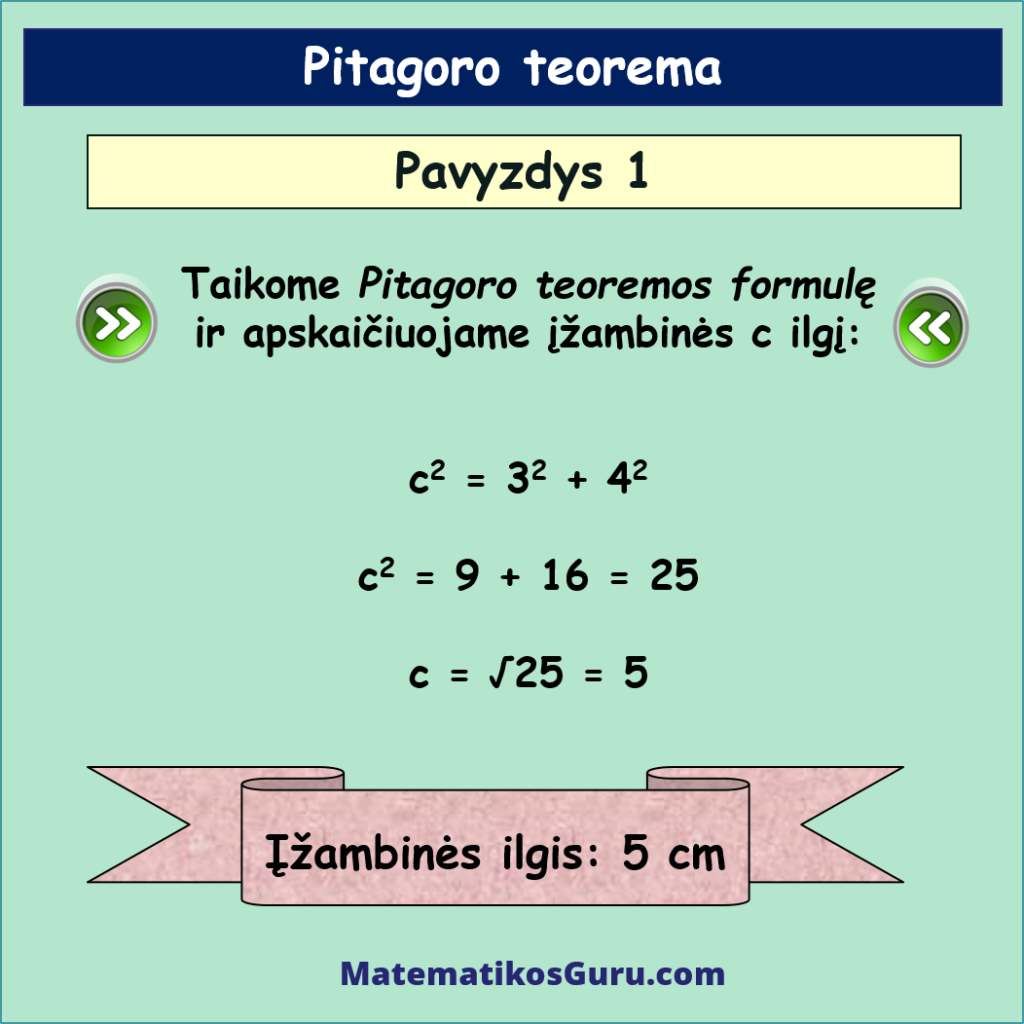
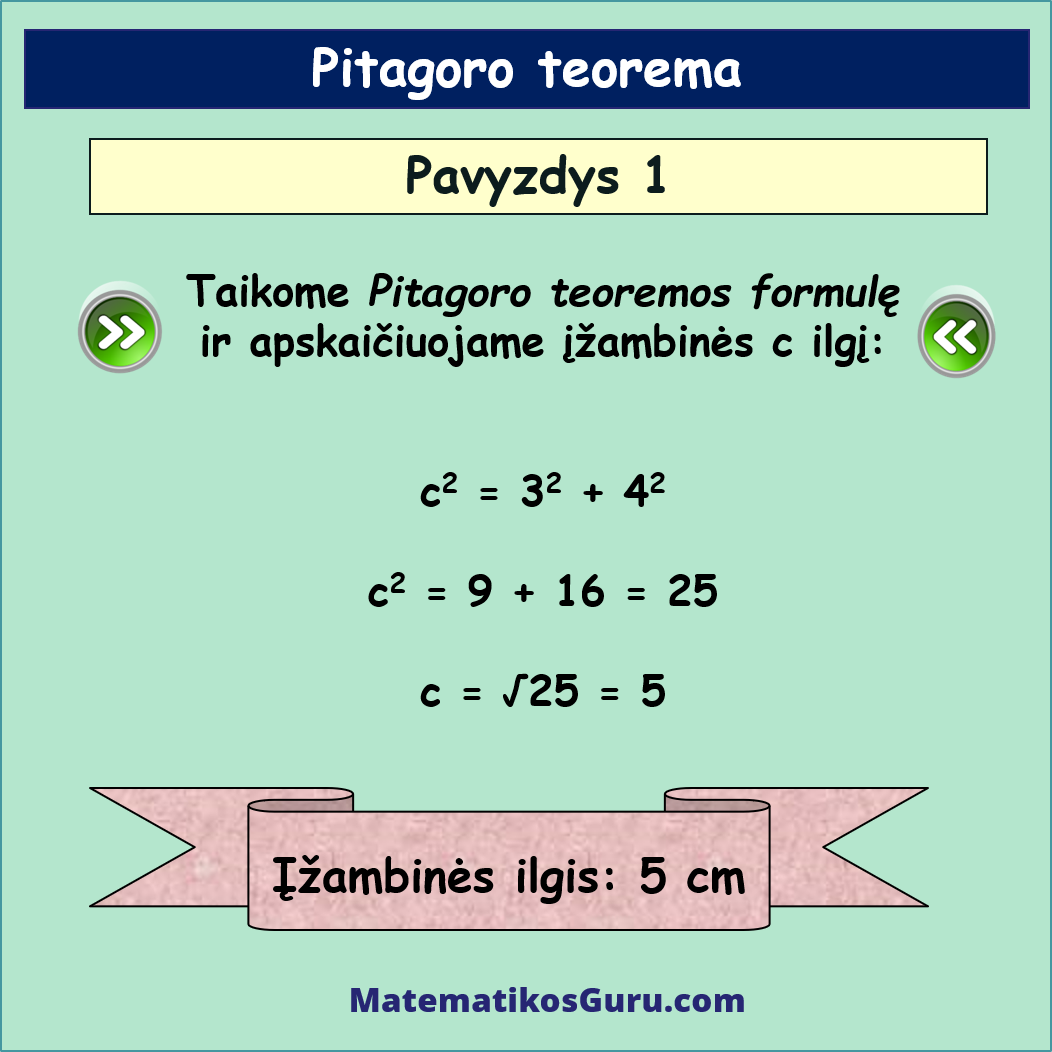
Taikome Pitagoro teoremos formulę ir apskaičiuojame įžambinės c ilgį:
- c2 = 32 + 42
- c2 = 9 + 16 = 25
- c = √25 = 5
![]() Pavyzdys 2:
Pavyzdys 2:
Stačiojo trikampio įžambinės ilgis – 13 cm, vieno iš statinių ilgis yra 5 cm. Apskaičiuokite šio trikampio antrojo statinio ilgį.
Pažymėkime vieną statinį raide a, o kitą – raide b, o įžambinę – raide c. Taikydami Pitagoro teoremą, gauname tokią lygtį: a2 + b2 = c2, kur:
- a – vieno iš statinių ilgis
- b – kito iš dviejų statinių ilgis
- c – įžambinės ilgis
Šiuo atveju, kadangi yra nežinomas vieno iš statinių ilgis (tarkime statinio b), išreikškime jį iš šios lygties, t.y.:
- b2 = c2 – a2
Taikome Pitagoro teoremos formulę ir apskaičiuojame statinio b ilgį:
- b2 = 132 – 52
- b2 = 169 – 25 = 144
- b = √144 = 12

Pitagoro teorema – vaizdinė medžiaga
Pitagoro teorema – video medžiaga
Populiariausios temos:
- Trikampio plotas, trikampio ploto formulė
- Pitagoro teorema
- Stačiojo trikampio plotas
- Apskritimo plotas
- Skritulio plotas
- Apskritimo ilgis
- Lygiagretainis
- Rombas
- Trapecija, trapecijos plotas
- Cilindro tūris (ritinio tūris)
- Kvadrato plotas
- Koordinatės
- Abscisė
- Statusis trikampis
- Lygiašonė trapecija
- Kūgio tūris
- Daugyba
- Dalyba
- Apskritimas
- Kūgis
- Diskriminantas, diskriminanto formulė
- Natūralieji skaičiai
- Matematikos formulės
- Laipsniai
- Mediana
- Moda
- Stačiakampio plotas
- Lygiašonis trikampis
- Lygiašonio trikampio plotas
- Lygiakraščio trikampio plotas
- Kubas
- Procentai
- Stačiakampis
- Taisyklingoji piramidė
- Greitosios daugybos formulės
- Proporcija
- Kvadratas
- Skritulys
- Rutulys
- Kitos temos
Grįžkite iš Pitagoro teorema į MatematikosGuru.com pradžią