Paprastoji trupmena
Paprastoji trupmena: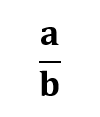 kur:
kur:
- a – sveikasis skaičius
- b – natūralusis skaičius
Skaičius a – trupmenos skaitiklis
Skaičius b – trupmenos vardiklis
Vardiklis b parodo, į kiek lygių dalių yra padalintas skaičius
Skaitiklis a parodo, kiek tokių dalių yra paimta
Paprastąją trupmeną dar galime užrašyti taip (dalmeniu):
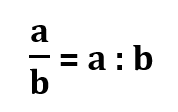
Ir atvirkščiai dalmenį galime užrašyti paprastąja trupmena:
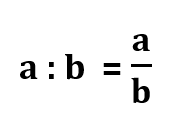
paprastoji trupmena yra:
- taisyklinga, jeigu |a| < |b|
- netaisyklinga, jeigu |a| ≥ |b|
Pagrindinė paprastosios trupmenos savybė
Paprastosios trupmenos skaitiklį ir daliklį padauginus ar padalinus iš to paties skaičiaus n, kuris nėra lygus 0, trupmenos reikšmė nepasikeičia:
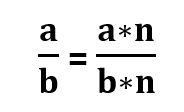
arba
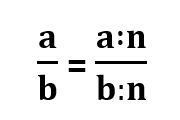
Paprastųjų trupmenų palyginimas
Kuomet lyginame dvi paprastąsias trupmenas, kurių vardikliai yra vienodi, didesnė yra ta, kurios skaitiklis yra didesnis:
jei a > b, tai:
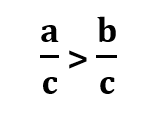
jei a < b, tai:
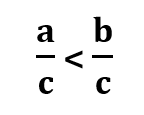
Jeigu norime palyginti trupmenas, kurių vardikliai yra skirtingi:
- šias trupmenas subendravardikliname
- ir tada jau galime lyginti gautas trupmenas pagal aukščiau nurodytas taisykles
Paprastųjų trupmenų sudėtis ir atimtis
Norėdami sudėti arba atimti paprastąsias trupmenas, kurių vardikliai yra vienodi, sudedame arba atimame jų skaitiklius, o vardiklis lieka tas pats:
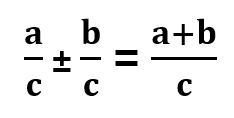
Jeigu norime sudėti arba atimti paprastąsias trupmenas, kurių vardikliai yra skirtingi:
- šias trupmenas subendravardikliname
- ir tada jau galime sudėti arba atimti gautas trupmenas su vienodais vardikliais pagal aukščiau nurodytas taisykles
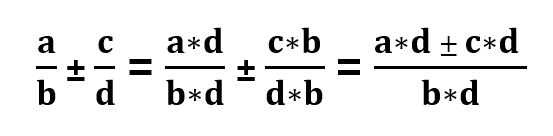
Paprastųjų trupmenų daugyba ir dalyba
Norėdami padauginti paprastąsias trupmenas, skaitiklį dauginame iš skaitiklio, o vardiklį dauginame iš vardiklio:
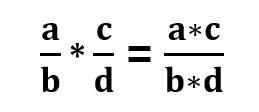
Norėdami padalinti paprastąsias trupmenas:
- dalybą keičiame daugyba, o antrosios trupmenos skaitiklį sukeičiame vietomis su vardikliu (kitaip tariant – antrąją trupmeną apverčiame)
- tuomet dauginame gautas trupmenas pagal trupmenų daugybos taisyklę
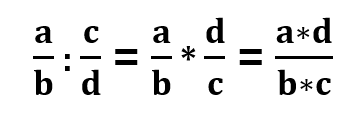
Daugindami ar dalindami paprastąsias trupmenas, visuomet tikriname, ar galime jas supaprastinti, taip pat tikriname, ar galime išskirti sveikąją dalį
Grįžkite iš Paprastosios trupmenos temos į MatematikosGuru.com pradžią