Lygčių sistemos sprendimas sudėties būdu

---

Dar vienas būdas, kaip galime spręsti lygčių sistemą, tai yra sudėties būdas

Taikydami šį būdą, turime atlikti tokius veiksmus:

1. Sudedame abi sistemos lygis panariui, t.y. x narius su x nariais ir y narius su y nariais
2. Išsprendžiame gautą lygtį, t.y. randame vieno iš lygčių sistemos nežinomojo reikšmę
3. Šią gautą vieno nežinomojo reikšmę įstatome į bet kurią lygčių sistemos lygtį
4. Randame kito nežinomojo reikšmę
5. Patikriname, ar gautos nežinomųjų reikšmės yra duotos lygčių sistemos sprendiniai

Svarbu: šį eiliškumą galime taikyti tik tuomet, kad sudėjus lygits panariui, gaunama lygtis su vienu nežinomuoju.

Jeigu taip nesigauna, tuomet turėsime taikyti ir keitimo būdą tam, kad galėtume išspręsti šią lygčių sistemą

---

1 pavyzdys

---

Panagrinėkime pavyzdį, kuomet gali būti taikoma aukščiau pateiktas eiliškumas:

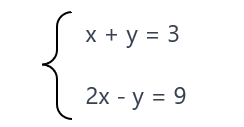
1 žingsnis:

 

Sudedame lygtis panariui

• x + 2x +y – y = 12
• 3x = 12

2 žingsnis:

 

Išsprendžiame gautą lygtį ir surandame nežinomojo x reikšmę

• x = 12/3 = 4

3 žingsnis:

 

Gautą nežinomojo x reikšmę įstatome į bet kurią duotos lygčių sistemos lygtį

• Pvz. į šią lygtį: x + y = 3
• 4 + y = 3

4 žingsnis:

 

Surandame kito nežinomojo reikšmę

• y = 3 – 4 = -1

5 žingsnis:

 

Patikriname, ar gautos nežinomųjų reikšmės yra duotos lygčių sistemos sprendiniai

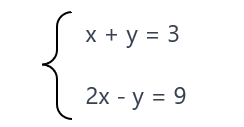
x = 4 , y = -1

Įstatome nežinomųjų reikšmes į pirmąją lygčių sistemos lygtį, t.y. x + y = 3, ir tikriname, ar lygtis teisinga

4 – 1 = 3, lygtis teisinga

Įstatome nežinomųjų reikšmes į antrąją lygčių sistemos lygtį, t.y. 2x – y = 9, ir tikriname, ar lygtis teisinga

2*4 – (-1) = 8 + 1 = 9, lygtis teisinga

Vadinasi nežinomųjų x ir y reikšmės, kai x = 4 ir y = -1, yra duotos lygčių sistemos sprendiniai

---

2 pavyzdys

---

Panagrinėkime pavyzdį, kai aukščiau pateiktas lygčių sistemos sprendimo eiliškumas negali būti nuosekliai taikomas, t.y. sudėjus lygtis panariui, nebegalime iš karto surasti vieno nežinomųjų reikšmę:

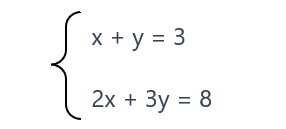
1 žingsnis:

 

Sudedame lygtis panariui

• 3x + 4y = 11

2 žingsnis:

 

Išsprendžiame gautą lygtį ir surandame nežinomojo x reikšmę – šio žingsnio nebegalime atlikti

Iš šios lygties nebegalime surasti vieno nežinomųjų reikšmę. Todėl toliau turime naudoti išreiškimo būdą, t.y.. turime išreikšti vieną nežinomąjį  kito nežinomojo atžvilgiu:

Pavyzdžiui, išreikškime x y atžvilgiu:

• x = (11 – 4y)/3

3 žingsnis:

 

Gautą nežinomojo x reikšmę įstatome į bet kurią duotos lygčių sistemos lygtį. Šiuo atveju naudojame vieno nežinomojo (x) išraišką kito nežinomojo atžvilgiu

Šią reikšmę įstatome į vieną iš lygčių sistemos lygčių ir surandame y reikšmę:

• (11 – 4y)/3 + y = 3

4 žingsnis:

 

Sprendžiamą gautą lygį

• (11 – 4y)/3 + y = 3

Padauginame visus narius iš 3 tam, kad panaikintume trupmeną

• 11 – 4y + 3y = 9

Sukeliame į vieną lygties pusę visus narius, kur yra nežinomasis, o į kitą puses visus narius, kur yra tik skaičiai

• -4y + 3y = 9 – 11

Supaprastiname ir apskaičiuojame y reikšmę:

• -y = -2
• y = 2

5 žingsnis:

 

Gautą nežinomojo y reikšmę įstatome į bet kurią duotos lygčių sistemos lygtį ir surandame kito nežinomojo (x) reikšmę

Pvz. į šią lygtį: x + y = 3

• x + 2 = 3
• x = 3 – 2 = 1

6 žingsnis:

 

Patikriname, ar gautos nežinomųjų reikšmės yra duotos lygčių sistemos sprendiniai

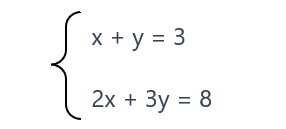
x = 1 , y = 2

Įstatome nežinomųjų reikšmes į pirmąją lygčių sistemos lygtį, t.y. x + y = 3, ir tikriname, ar lygtis teisinga

1 + 2 = 3, lygtis teisinga

Įstatome nežinomųjų reikšmes į antrąją lygčių sistemos lygtį, t.y. 2x + 3y = 8 ir tikriname, ar lygtis teisinga

2*1 +3*2 = 2 + 6 = 8, lygtis teisinga

Vadinasi nežinomųjų x ir y reikšmės, kai x = 1 ir y = 2, yra duotos lygčių sistemos sprendiniai

---

Populiariausios temos:

---

Grįžkite iš Kvadratinių šaknų sudėtis – √a+√a temos į MatematikosGuru.com pradžią