Diskriminantas – diskriminanto formulė
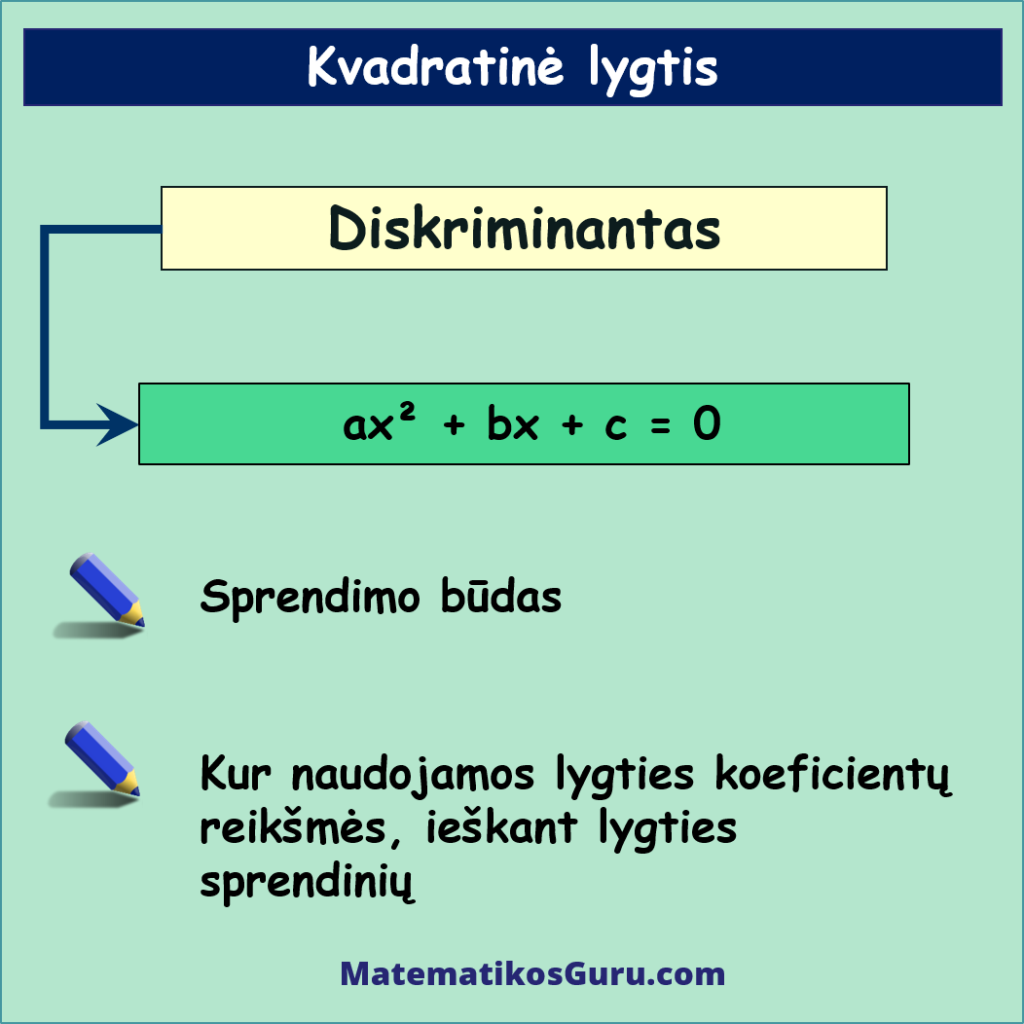
Vienas iš galimų kvadratinės lygties ax² + bx + c = 0 sprendimo būdų yra susijęs su šios lygties koeficientų reikšmių naudojimu, ieškant lygties sprendinių.
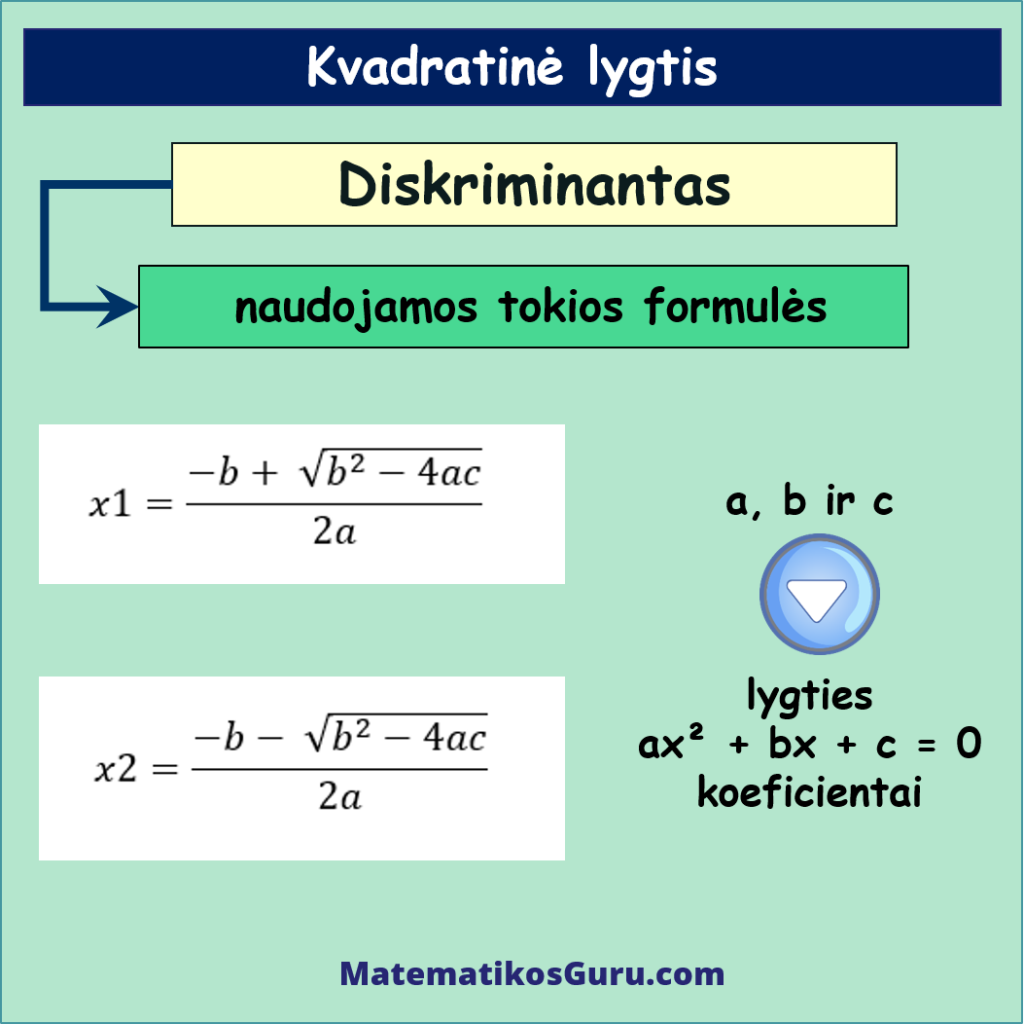
Kvadratinės lygties ax² + bx + c = 0 sprendinius galima apskaičiuoti naudojant formules:
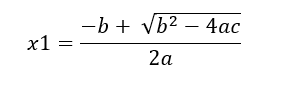
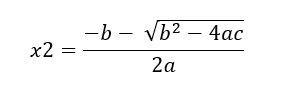
Šiose formulėse a, b ir c yra lygties ax² + bx + c = 0 koeficientai
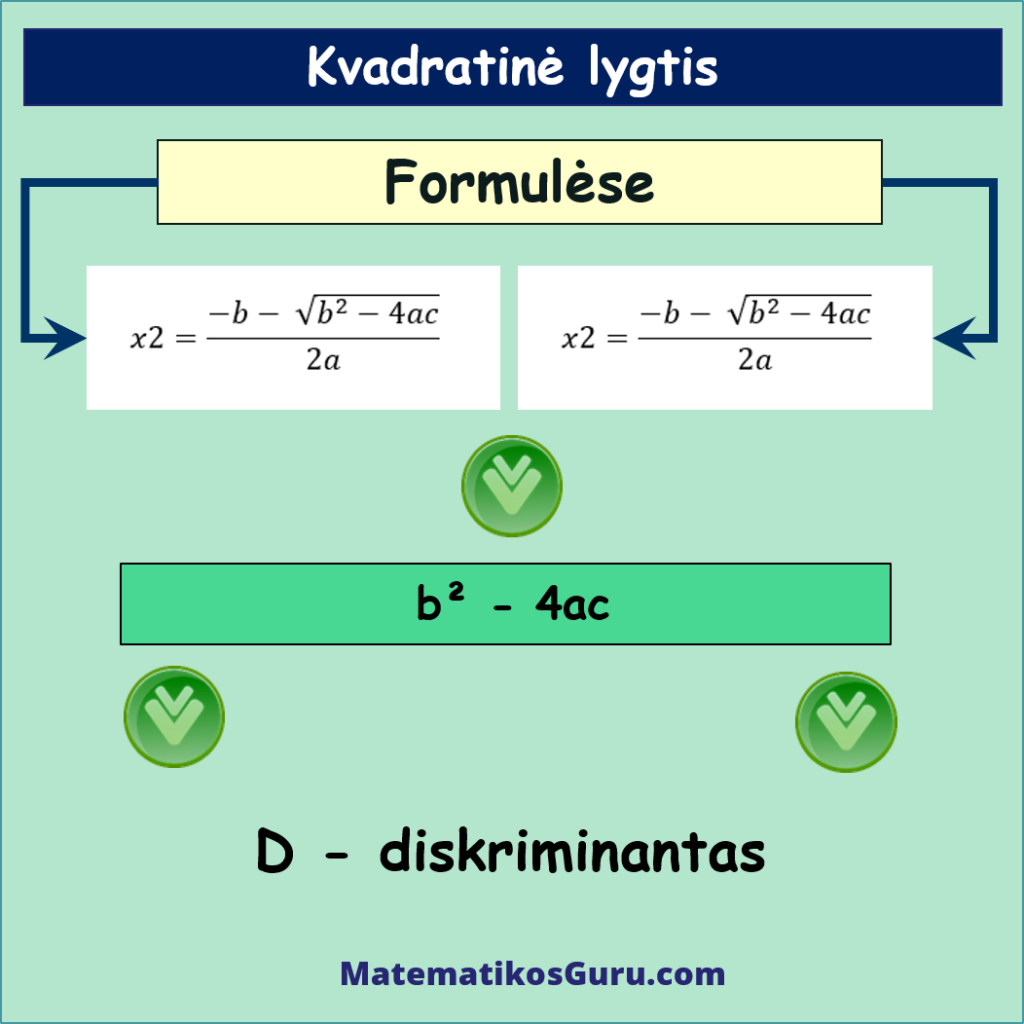
Šių formulių reiškinys b² – 4ac vadinamas diskriminantu ir žymimas raide D. Tai ir yra diskriminanto formulė, t.y.:
D = b² – 4ac
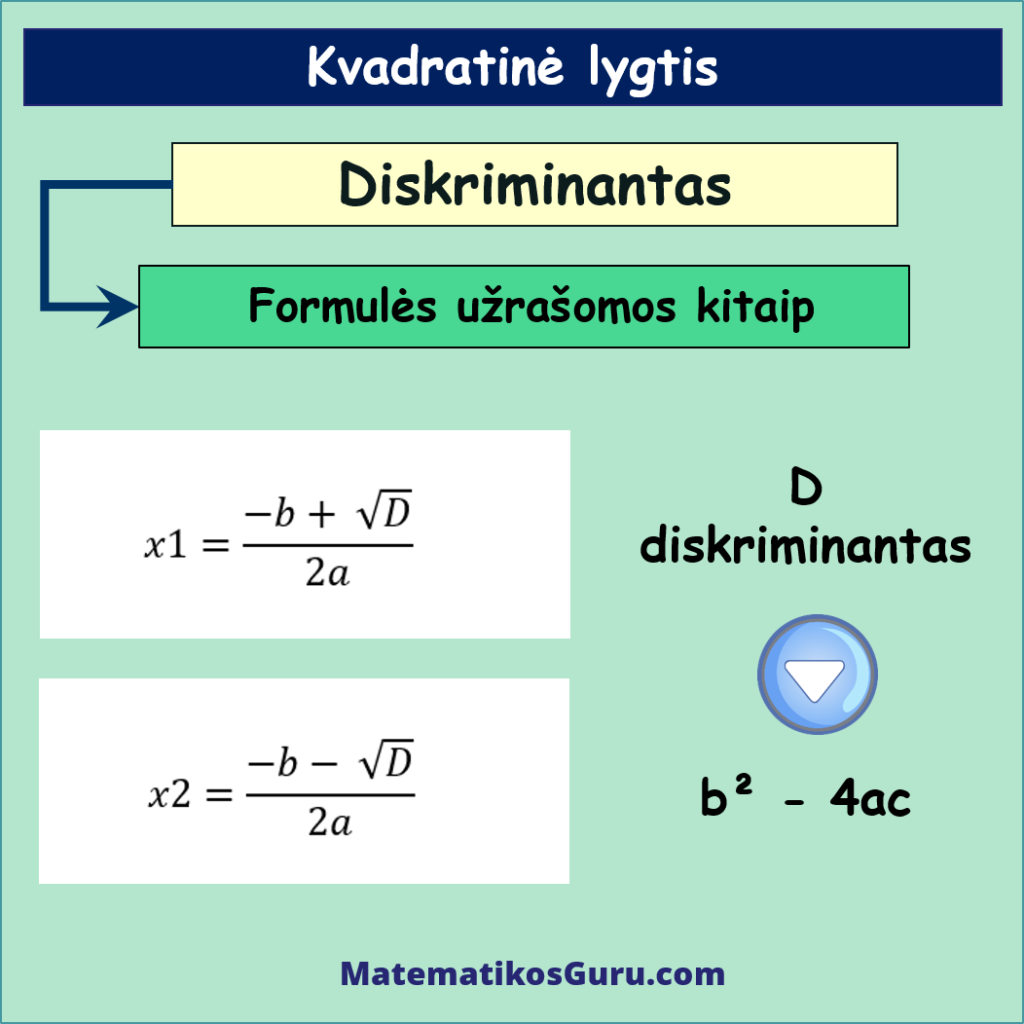
Dar kitaip kvadratinės lygties ax² + bx + c = 0 sprendinių apskaičiavimo formules galime užrašyti taip:
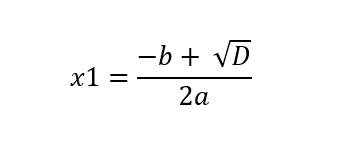
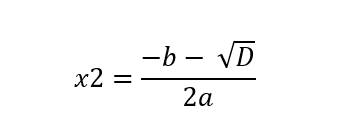
D šiose formulėse yra diskriminantas, kuris apskaičiuojamas pagal diskriminanto formulę: b² – 4ac
Diskriminantas – pavyzdys
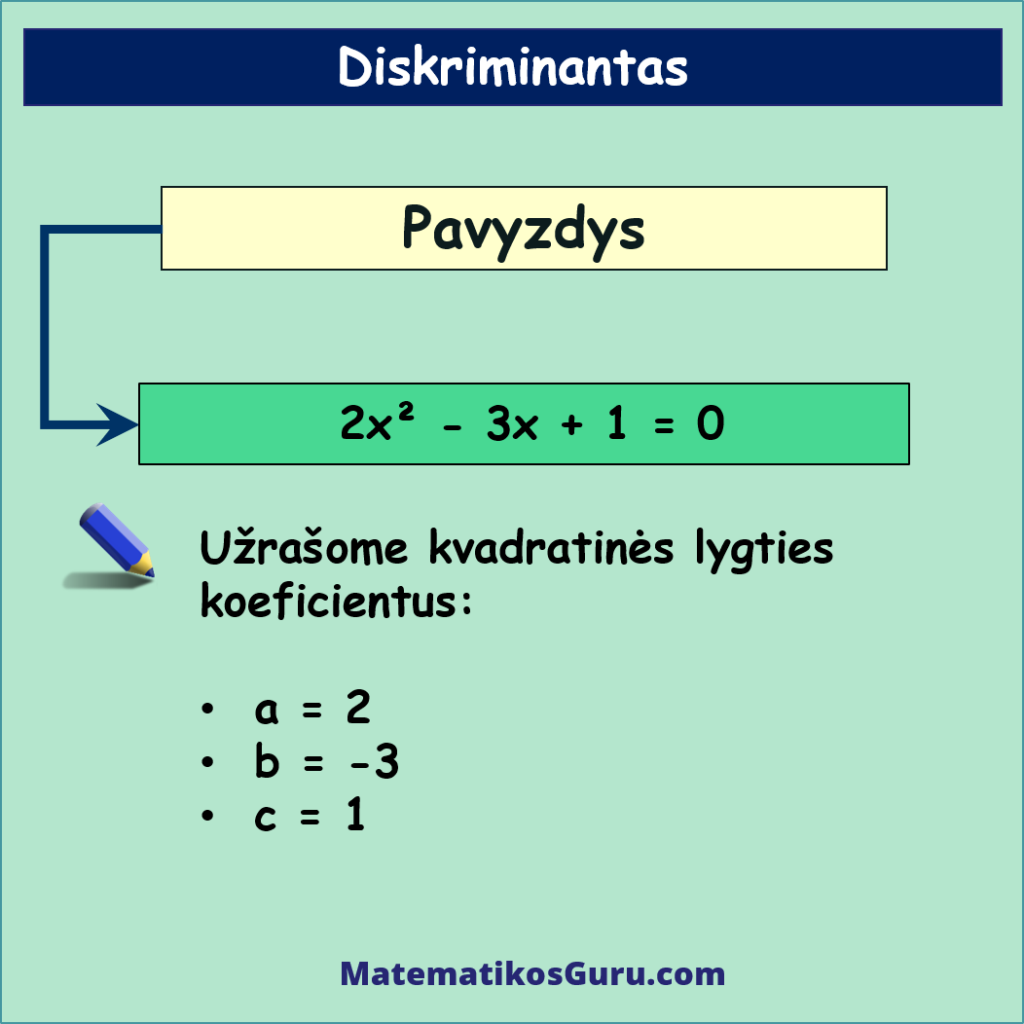
Išnagrinėkime pagal pavyzdį, kokius veiksmus reikia atlikti, norint išspręsti kvadratinę lygtį, naudojant duotas formules ir diskriminanto formulę, pvz. 2x² – 3x + 1 = 0
- Nurodome lygties koeficientus a, b, c, t.y.:
-
- a = 2
- b = -3
- c = 1
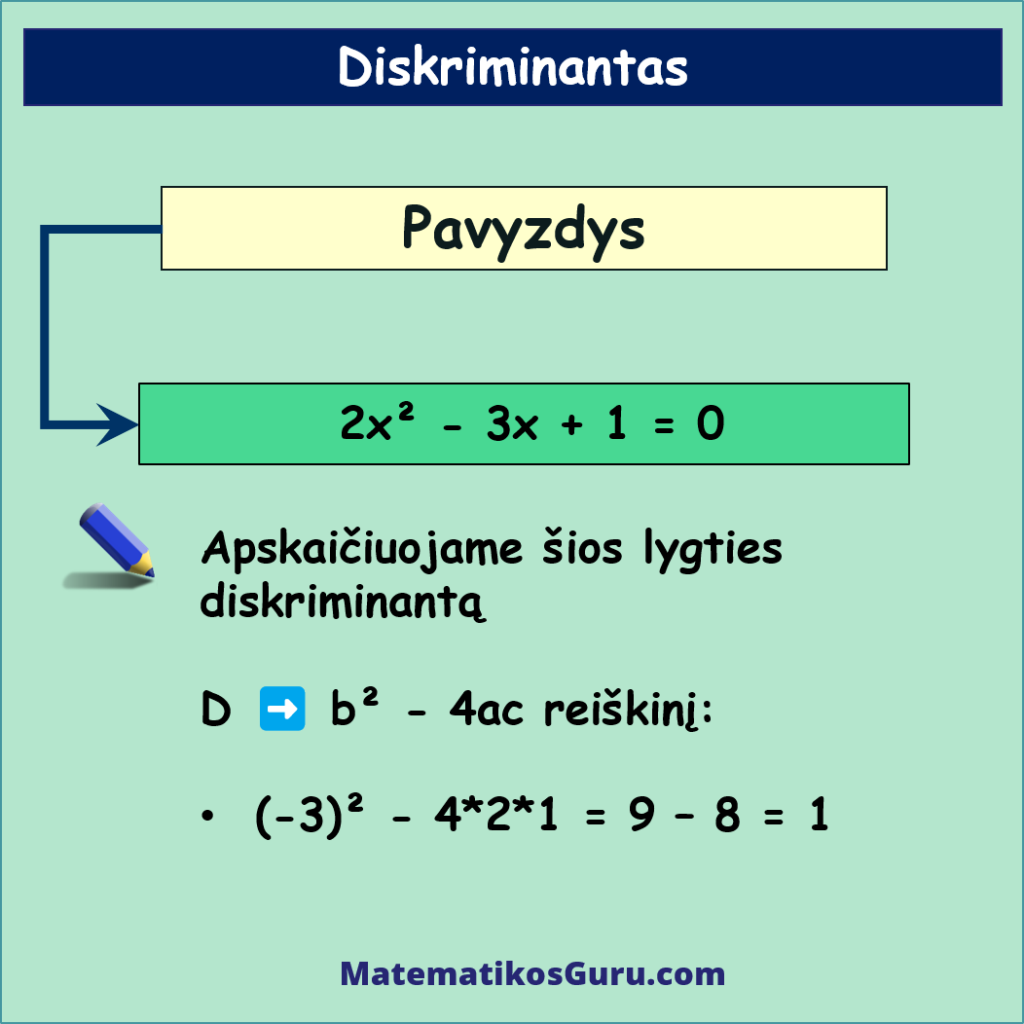
- Apskaičiuojame šios lygties diskriminantą D, t.y. b² – 4ac reiškinį, t.y.:
-
- (-3)² – 4*2*1 = 9 – 8 = 1
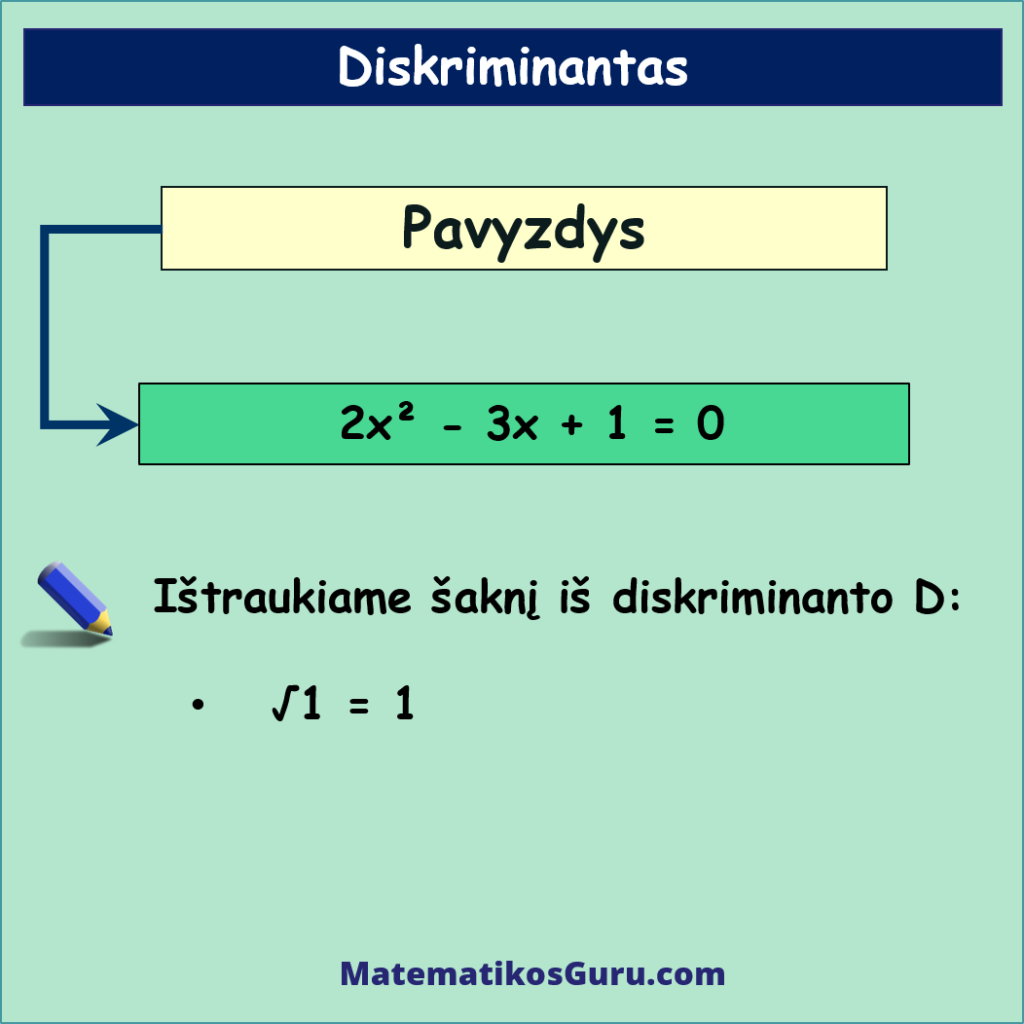
- Ištraukiame šaknį iš diskriminanto D, t.y.:
-
- √1 = 1
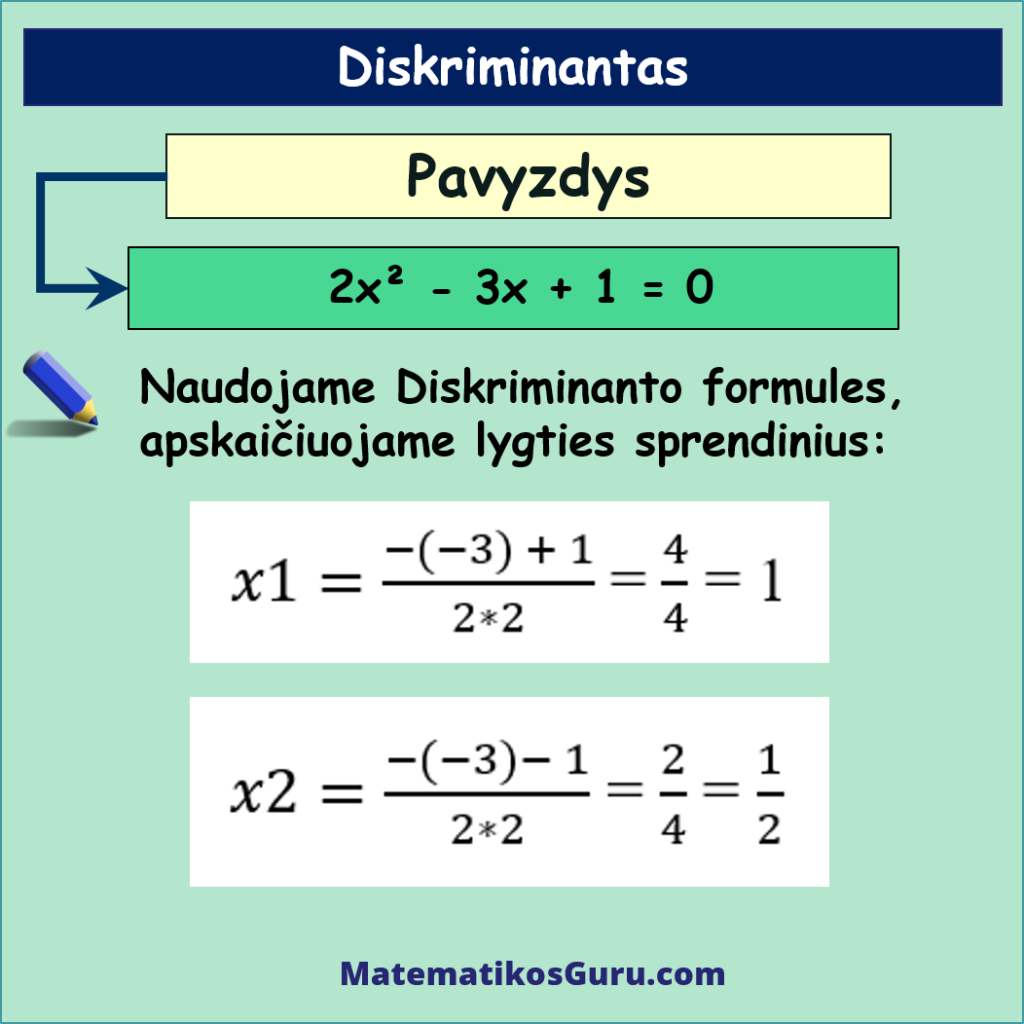
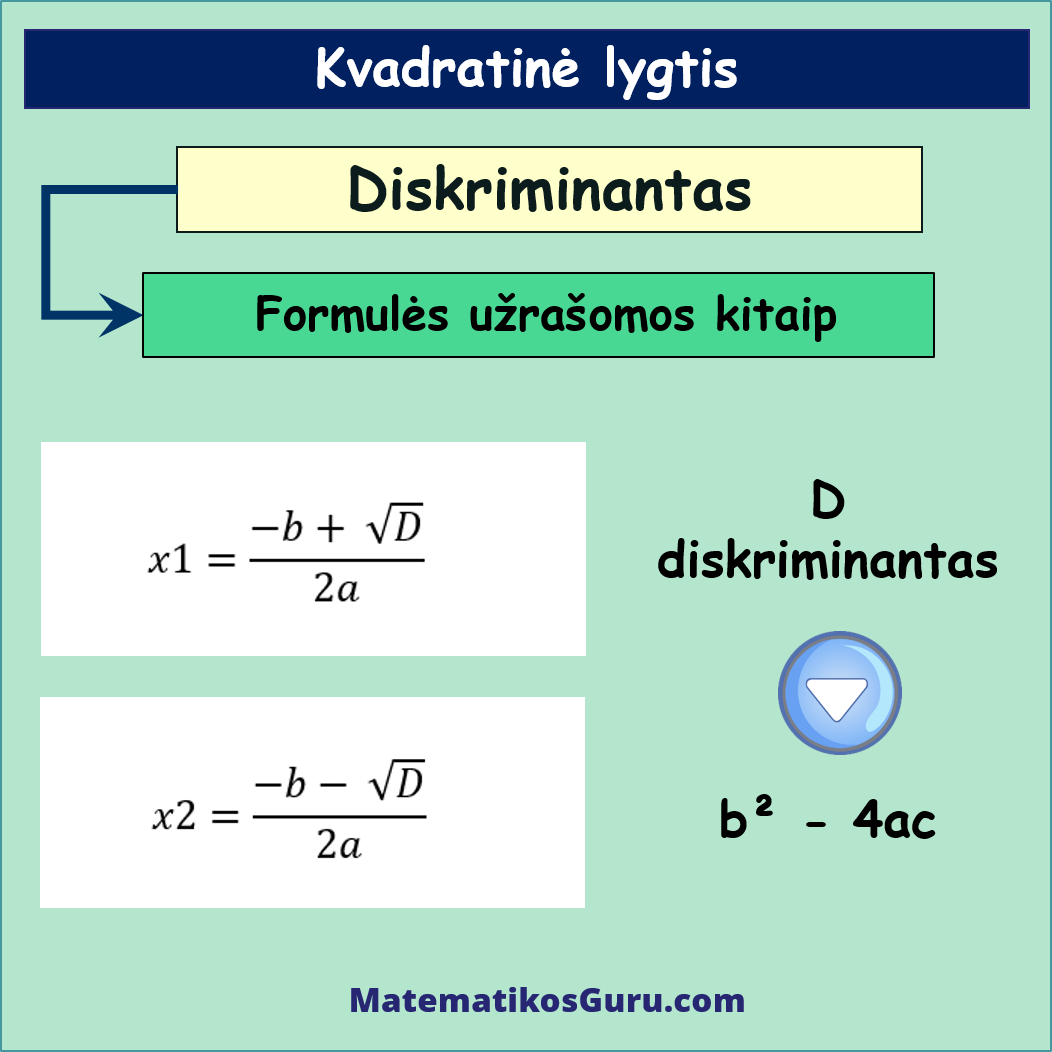
- Naudodami kvadratinės lygties sprendinių apskaičiavimo formules, kur naudojamas diskriminantas, apskaičiuojame lygties sprendinius:
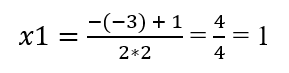
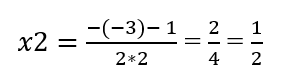
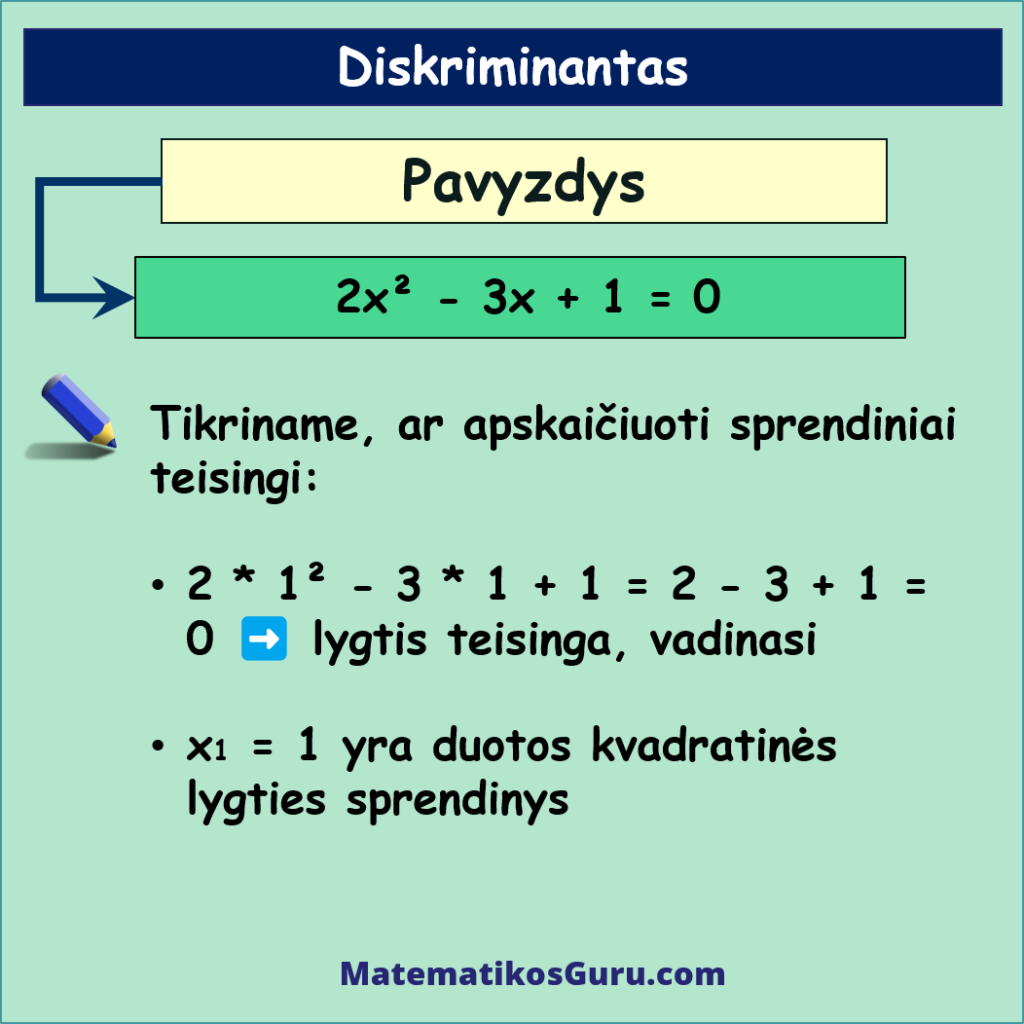
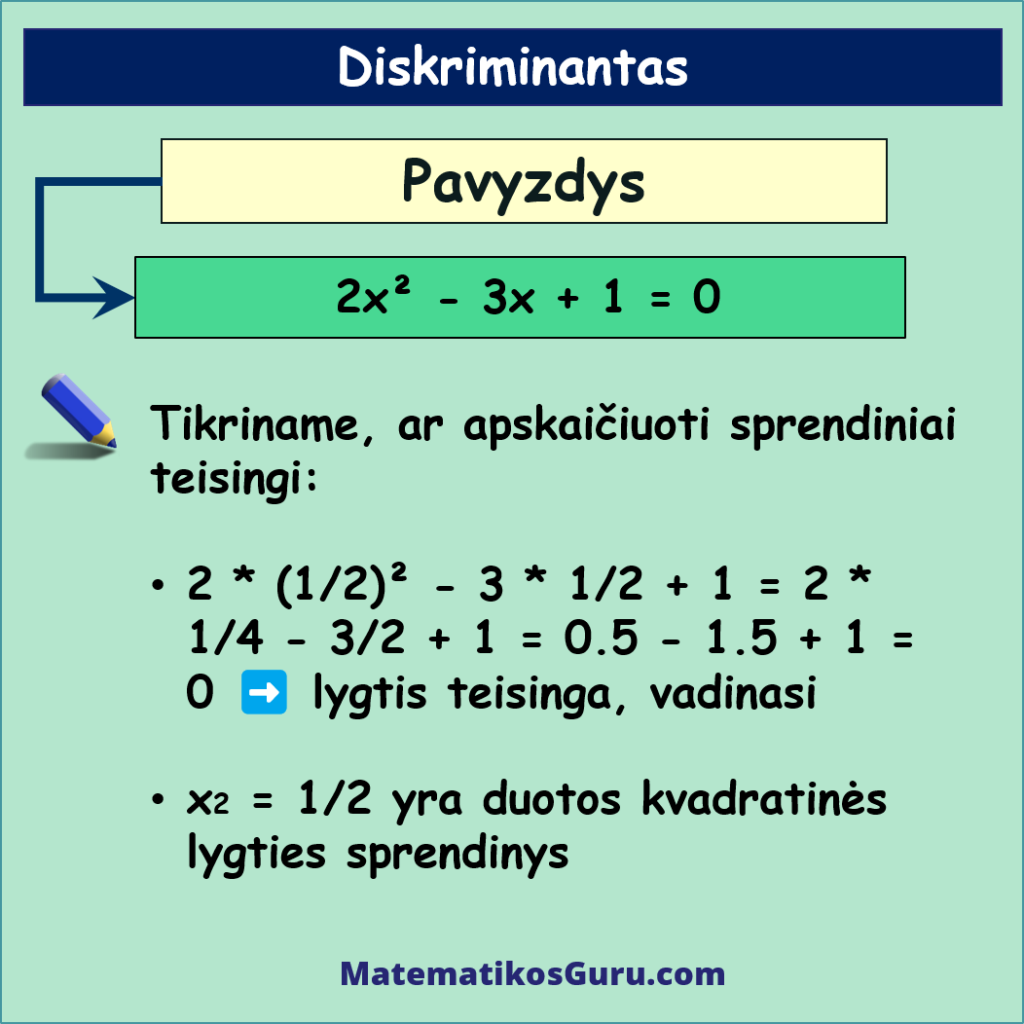
Įstatydami šiuos sprendinius į duotą kvadratinę lygį 2x² – 3x + 1 = 0, galite patikrinti, ar sprendiniai teisingi.
- 2 * 1² – 3 * 1 + 1 = 2 – 3 + 1 = 0 ➡️ lygtis teisinga, vadinasi x1 = 1 yra duotos kvadratinės lygties sprendinys
- 2 * (1/2)² – 3 * 1/2 + 1 = 2 * 1/4 – 3/2 + 1 = 0.5 – 1.5 + 1 = 0 ➡️ lygtis teisinga, vadinasi x2 = 1/2 yra duotos kvadratinės lygties sprendinys
Kvadratinės lygties sprendinių skaičius
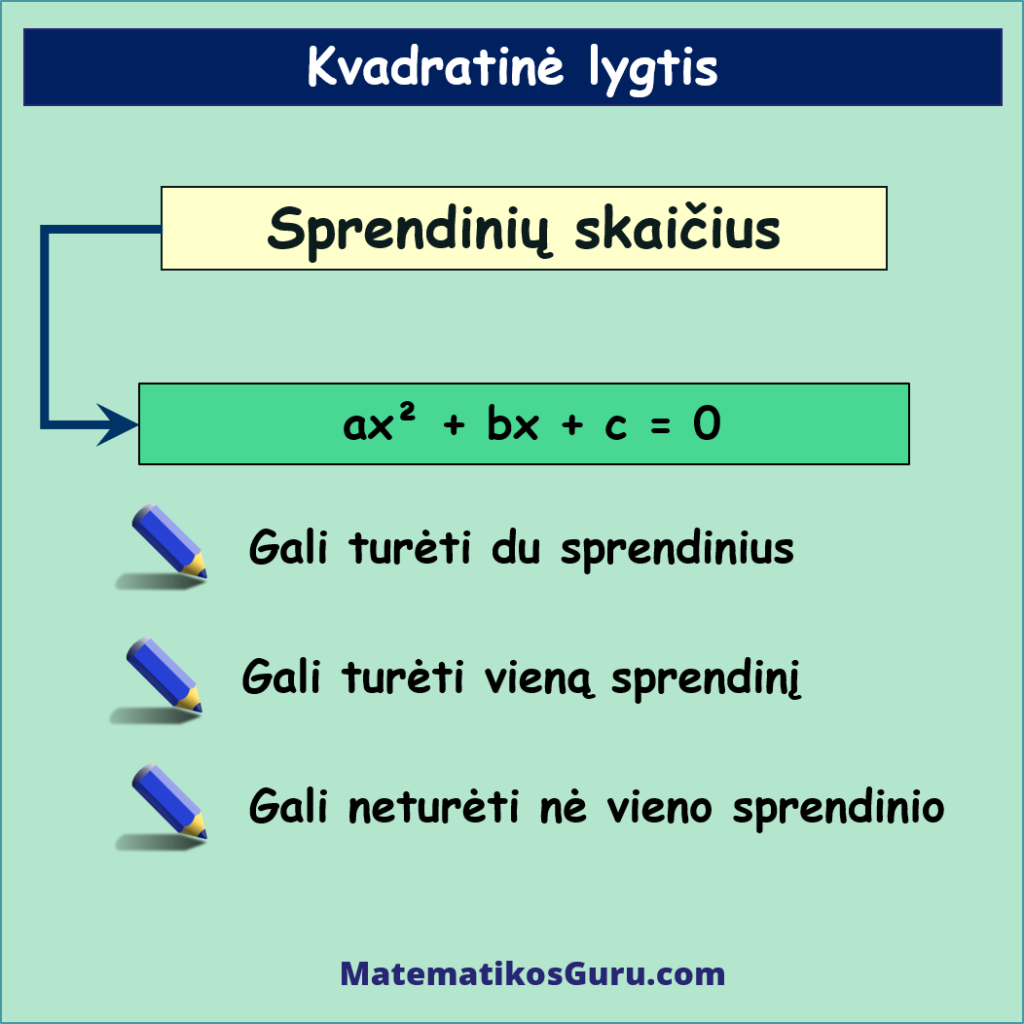
Kiek sprendinių turi kvadratinė lygtis ax² + bx + c = 0?
Ši lygtis:
- Gali turėti du sprendinius
- Gali turėti vieną sprendinį
- Gali neturėti nė vieno sprendinio
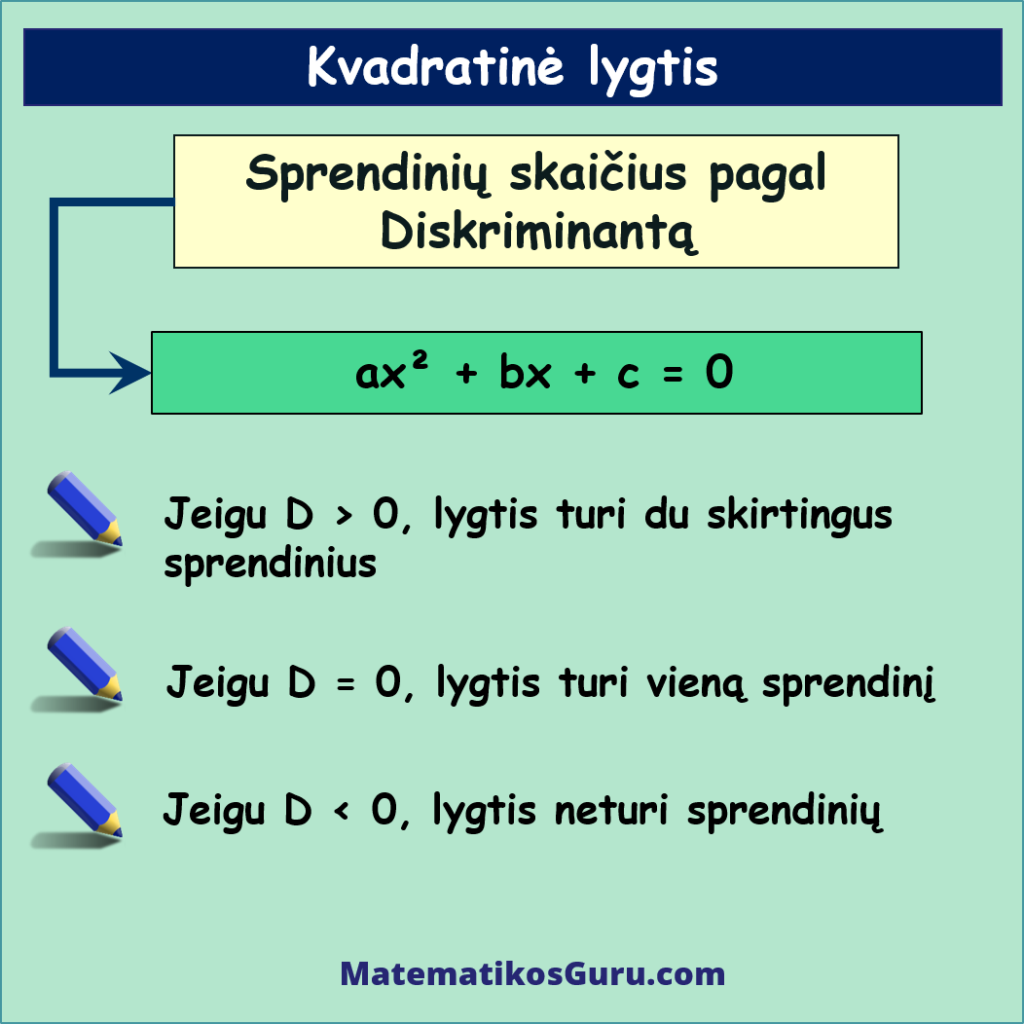
Pagal kvadratinės lygties diskriminantą galime nustatyti, kiek sprendinių turi lygtis, t.y.:
- Jeigu D > 0, lygtis turi du skirtingus sprendinius
- Jeigu D = 0, lygtis turi vieną sprendinį
- Jeigu D < 0, lygtis neturi sprendinių
Tam, kad galima būtų išspręsti sudėtingas kvadratines lygtis, turime jas pertvarkyti į šią lygties formą: ax² + bx + c = 0
Video medžiaga:
Visa vaizdinė medžiaga:
Populiariausios temos:
- Trikampio plotas, trikampio ploto formulė
- Pitagoro teorema
- Stačiojo trikampio plotas
- Apskritimo plotas
- Skritulio plotas
- Apskritimo ilgis
- Lygiagretainis
- Rombas
- Trapecija, trapecijos plotas
- Cilindro tūris (ritinio tūris)
- Kvadrato plotas
- Koordinatės
- Abscisė
- Statusis trikampis
- Lygiašonė trapecija
- Kūgio tūris
- Daugyba
- Dalyba
- Apskritimas
- Kūgis
- Diskriminantas, diskriminanto formulė
- Natūralieji skaičiai
- Matematikos formulės
- Laipsniai
- Mediana
- Moda
- Stačiakampio plotas
- Lygiašonis trikampis
- Lygiašonio trikampio plotas
- Lygiakraščio trikampio plotas
- Kubas
- Procentai
- Stačiakampis
- Taisyklingoji piramidė
- Greitosios daugybos formulės
- Proporcija
- Kvadratas
- Skritulys
- Rutulys
- Kitos temos
Grįžkite iš Kvadratinės lygties sprendinių formulė, diskriminantas temos į MatematikosGuru.com pradžią