Kvadaratinė lygtis ax² + bx + c = 0 (kur a ≠ 0) gali turėti du skirtingus sprendinius, vieną sprendinį arba nė vieno
Tai galime nustatyti pagal kvadratinės lygties diskriminantą:
- Kai lygties ax² + bx + c = 0 (kur a ≠ 0) diskriminantas D > 0, lygits turi du sprendinius
- Kai lygties ax² + bx + c = 0 (kur a ≠ 0) diskriminantas D = 0, lygits turi vieną sprendinį
- Kai lygties ax² + bx + c = 0 (kur a ≠ 0) diskriminantas D < 0, lygits neturi sprendinių
Pavyzdžiui, duota tokia kvadratinė lygtis:
- 3x² – 17x + 4 = 0
Kiek ji turi sprendinių?
Norėdami nustatyti, kiek ši kvadratinė lygtis turi sprendinių, apskaičiuojame šios lygties diskriminantą:
D = b² – 4ac = (-17)² – 4*3*4 = 289 – 48 = 241
Kadangi D > 0, ši lygtis turi du sprendinius
Sudėtingesnės kvadratinės lygtys
 Tuo atveju, jeigu duota sudėtingesnė lygtis, ją visų pirma būtina pertvarkyti į tokio formato lygį: ax² + bx + c = 0
Tuo atveju, jeigu duota sudėtingesnė lygtis, ją visų pirma būtina pertvarkyti į tokio formato lygį: ax² + bx + c = 0
Ir tuomet jau galima spręsti, taikant kvadratinių lygčių sprendimo būdus.
Pavyzdžiui, duota tokia kvadratinė lygtis:
- x² + x = 24 – 4x
1. Norėdami ją išspręsti, pertvarkome į tinkamo formato lygį:
- x² + x + 4x – 24 = 0
- x² + 5x – 24 = 0
2. Sprendžiame šią lygtį, naudodami diskriminantą ir kvadratinių lygčių sprendimo formules
D = b² – 4ac
Apskaičiuojame diskriminantą:
D = 5² – 4*1*(-24) = 25 +96 = 121
Kadangi D > 0, ši lygtis turi du sprendinius.
3. Naudojame šias kvadratinių lygčių sprendinių apskaičiavimo formules ir ieškome duotos lygties sprendinių x1 ir x2. Šiose formulėse naudosime apskaičiuotą diskriminanto reikšmę:
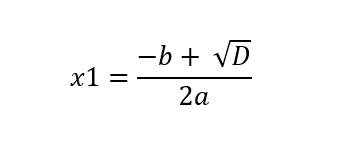
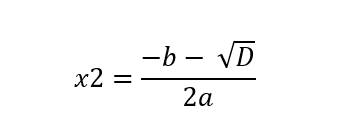
Naudodami kvadratinių lygčių sprendimo formules, apskaičiuojame lygties sprendinius:
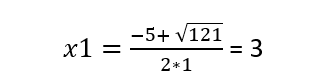
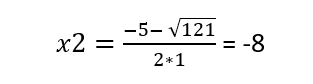
Lygtis x² + x = 24 – 4x turi du sprendinius:
- x1 = 3
- x2 = -8
Patikriname, ar šie sprendiniai ir yra duotos x² + x = 24 – 4x lygties sprendiniai:
3² + 3 = 24 – 4*3. Rezultatas: 12 = 12, lygybė teisinga, vadinasi x1 = 3 yra duotos kvadratinės lygties sprendinys
(-8)² + (-8) = 24 – 4*(-8). Rezultatas: 56 = 56, lygybė teisinga, vadinasi x2 = -8 yra duotos kvadratinės lygties sprendinys
Populiariausios temos:
- Trikampio plotas, trikampio ploto formulė
- Pitagoro teorema
- Stačiojo trikampio plotas
- Apskritimo plotas
- Skritulio plotas
- Apskritimo ilgis
- Lygiagretainis
- Rombas
- Trapecija, trapecijos plotas
- Cilindro tūris (ritinio tūris)
- Kvadrato plotas
- Koordinatės
- Abscisė
- Statusis trikampis
- Lygiašonė trapecija
- Kūgio tūris
- Daugyba
- Dalyba
- Apskritimas
- Kūgis
- Diskriminantas, diskriminanto formulė
- Natūralieji skaičiai
- Matematikos formulės
- Laipsniai
- Mediana
- Moda
- Stačiakampio plotas
- Lygiašonis trikampis
- Lygiašonio trikampio plotas
- Lygiakraščio trikampio plotas
- Kubas
- Procentai
- Stačiakampis
- Taisyklingoji piramidė
- Greitosios daugybos formulės
- Proporcija
- Kvadratas
- Skritulys
- Rutulys
Grįžkite iš Kvadratinės lygties sprendinių skaičius temos į MatematikosGuru.com pradžią