Skritulio plotas, skritulio ploto formulė

Pradėkime nuo to, kas yra skritulys

Skritulys ir apskritimas yra tarpusavyje susijusios sąvokos. Svarbu tai, kad apskritimas ir skritulys nėra tas pas.

Apskritimas – yra linija, kuri suformuoja geometrinę figūrą, išsidėsčiusią plokštumoje. Šią figūrą sudaro taškai, kurie yra vienodai nutolę nuo vieno plokštumos taško. Šis taškas vadinamas apskritimo centru. Apskritimo ilgis – tai atstumas aplink apskritimo ribą. Šis ilgis žymimas raide C

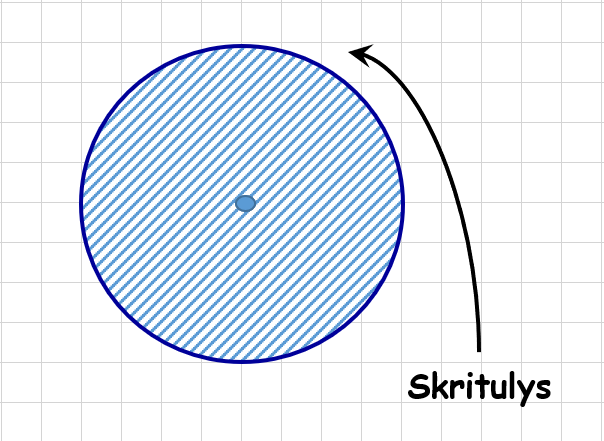
Skritulys – taip plokštumos dalis, kurią apriboja apskritimas. Visi plokštumos taškai, kurie yra apskritimo viduje priklauso skirtuliui. Skritulio centras, taip pat kaip ir apskritimo, žymimas raide C

skritulys

Apskritimo plotas negali būti apskaičiuotas, kadangi apskritimas – tai linija. Tad dažnai yra painiojamos sąvokos: Apskritimo plotas ir Skritulio plotas

Skaičiuojame skritulio (t.y. plokštumos dalies, kurią apriboja apskritimas) plotą, o ne apskritimo plotą

Analogiškai, negali būti apskaičiuotas skritulio ilgis, kadangi skritulys yra plokštumos dalis. Šiuo atveju skaičiuojamas apskritimo ilgis

Skritulio perimetras iš esmės yra apskritimo, kuris apriboją plokštumos dalį, vadinama skirtuliu, ilgis

Skritulio plotas

Toliau panagrinėkime, kaip apskaičiuojamas skirtulio plotas

Tolesniems skaičiavimams dar bus reikalingos tokios sąvokos:

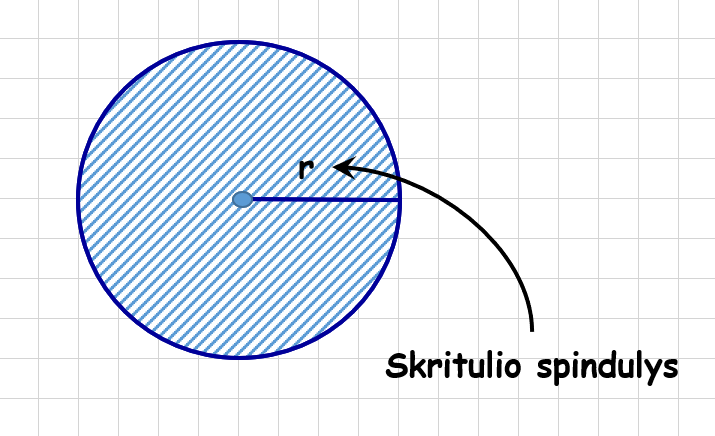
Skirtulio spindulys – atkarpa, kuri jungia bet kurį skritulio ribos (apskritimo, kurios riboją skritulį) tašką su skritulio centru. Skirtulio spindulio ilgis – yra šios atkarpos ilgis. Spindulys žymimas raide r arba R

skritulio spindulys

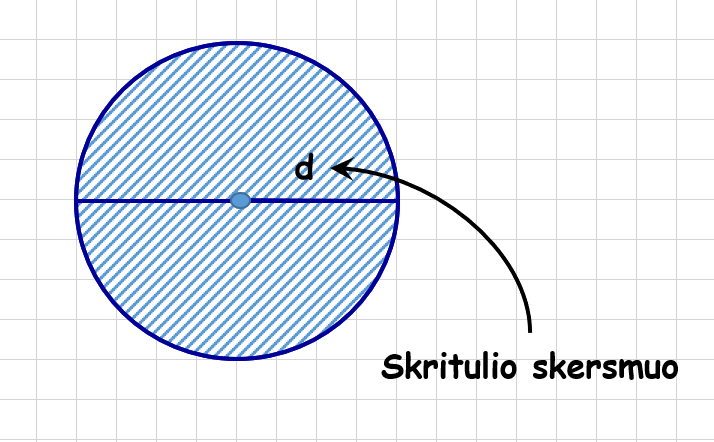
Skirtulio skersmuo – atkarpa, kuri eina per skritulio centrą ir jungia du skritulio ribos (apskritimo, ribojančio skritulį) taškus. Šios atkarpos ilgis (skersmens ilgis) žymimas d arba D

skritulio skersmuo

Yra du būdai, priklausomai nuo to, kokią turime informaciją

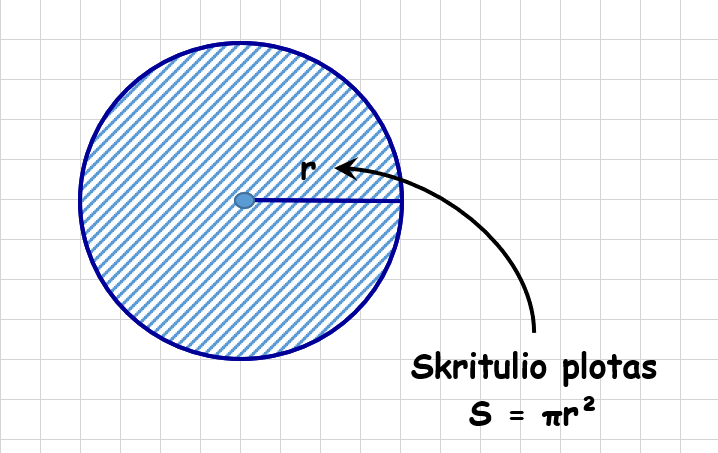
Skritulio ploto formulė, kai žinomas skritulio spindulys

Jeigu žinome skritulio spindulį, skritulio plotą apskaičiuojame taip:

S = πr²

π – yra pastovus dydis (konstanta), ir lygus 3,14

r – skritulio spindulio ilgis

skritulio plotas

Pavyzdžiui: duotas skritulys, kurio spindulio ilgis yra 5 cm. Naudodami skritulio ilgio formulę, kai yra žinomas skritulio spindulio ilgis, apskaičiuojame duoto skritulio plotą taip:

S=πr² = 3,14*5² = 78,5cm²

Skritulio ploto formulė, kai žinomas skritulio skersmuo

Kaip apskaičiuoti skritulio plotą, jeigu žinome skritulio skersmens ilgį?

Skritulio plotą apskaičiuojame taip:

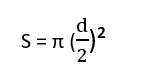
skritulio plotas formulė

π – yra pastovus dydis (konstanta), ir lygus 3,14

d – skritulio skersmens ilgis

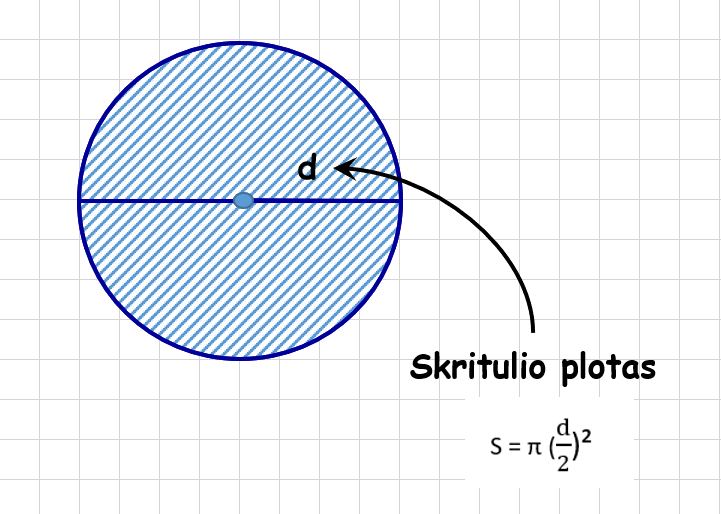
Pavyzdžiui: duotas skritulys, kurio skersmens ilgis yra 14 cm. Naudodami skritulio ploto formulę, kai yra žinomas skritulio skersmens ilgis, apskaičiuojame duoto skritulio plotą taip:

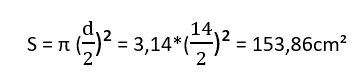
skritulio plotas formulė