Matematikos Guru

Išmokite matematiką kartu su Matematikos Guru

Apskritimo lygtis




Tarkime, kad turime apskritimą, kurio centras yra taške M0(x0, y0) (duotos apskritimo centro taško koordinatės koordinačių plokštumoje)

Pažymėkime apskritimo spindulį raide R

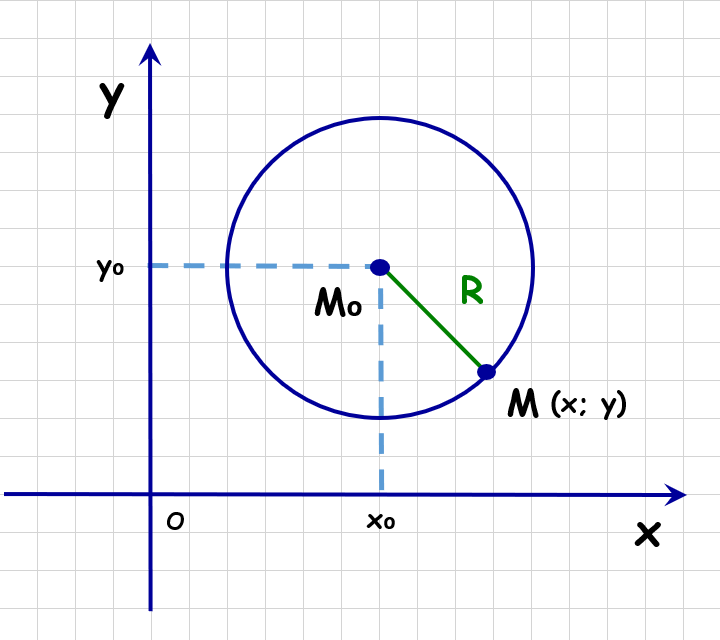
apskritimo lygtis

Pažymėkime M(x, y) tam tikrą tašką, priklausantį apskritimui

Atkarpos M0M ilgis atitiks apskritimo spindulio R ilgį

Prisimename, kaip apskaičiuojamas koordinačių plokštumoje esančios atkarpos ilgis, kai žinomos atkarpos galų taškų koordinatės:

▶️ (x − x0)2 + (y − y0)2 = R2, kur

  • x ir y – apskritimo taško M koordinatės
  • x0 ir y0 – apskritimo centro M0 koordinatės
  • R – apskritimo spindulys R

▶️ Ši lygtis vadinama bendrąja apskritimo lygtimi

Apskritimo centras yra koordinačių plokštumos pradžioje

Jei apskritimo centras yra koordinačių pradžioje O(0, 0), gauname paprasčiausią apskritimo lygtį:

▶️ Lygtis: x2 + y2 = R2

Pavyzdys

Apskritimo, kurio centras O(a, b) ir spindulys R > 0, lygtis yra:

▶️ (x − a)2 + (y − b)2 = R2

Pavyzdys: Lygtis x2 + y2 = 9 yra tokio apskritimo lygtis, kur:

  • Apskritimo centro koordinatės yra: a = 0 ir b = 0
  • Spindulio R ilgis – 3

Apskritimo lygties sprendiniai

  • Lygtis su dviem nežinomaisiais turi sprendinius – poras (x, y), su kuriomis lygtis tampa teisinga skaitine lygybe
  • Tuo atveju, jeigu duota bendroji apskritimo lygtis (x − a)2 + (y − b)2 = R2 jos sprendiniais bus x ir y poros, kurios tenkins šią lygtį

Šios temos uždaviniai VBE I metu gali būti įvairūs:

  • bus duota bendroji apskritimo lygtis ir turėsite rasti apskritimo centro koordinates
  • bus duota bendroji apskritimo lygtis ir turėsite rasti apskritimo spindulio ilgį
  • bus duota informacija apie apskritimo centrą ir jo tašką ar taškus, reikės užrašyti bendrąją apskritimo lygtį

Uždaviniai

Tai yra tipiniai VBE I uždaviniai – spręsk ir ruoškis:

────────

➡️ Uždavinys 1:

Koordinačių plokštumoje esančio apskritimo centras yra taškas A(k; −2). Šio apskritimo spindulio ilgis lygus 4, o apskritimo lygtis yra. x2 + y2 − 2kx + 4y = 0. Nustatykite k2 reikšmę

────────

➡️ Uždavinys 2:

Duota apskritimo lygtis x2 + y2 + 2mx + 2py = c (čia c > 0). Kuris iš pateiktų taškų yra šio apskritimo centras? Pažymėkite teisingą atsakymą.

a. (p; m)

b. (−m; −p)

c. (m; p)

d. (−p; −m)

────────

➡️ Uždavinys 3:

Duota apskritimo lygtis x2 + y2 − 6x + 12y + 20 = 0. Kam lygus šio apskritimo spindulio ilgis?

────────

➡️ Uždavinys 4:

Apskritimo centras yra taškas O(1; 0), o spindulys R = √17. Taškas A(2; t) priklauso apskritimui; čia t > 0. Apskaičiuokite t reikšmę

Populiariausios temos:

Grįžkite iš Apskritimo lygtis temos į MatematikosGuru.com pradžią